GAMES101 作业0

发表于 2024/11/02

作者 Wang Simiao

14 分钟阅读

GAMES101 作业0

上次学习GAMES101是在大三, 但是由于作业要求是用虚拟机+Ubuntu, 我嫌太麻烦, 就不想做作业了, 但是经过这两年的学习, 我觉得不动手实践是学不会的, 所以这次我决定丛头开始, 把作业和课程都再学习一遍

我的所有GAMES101作业的仓库地址: GAMES101-Assignments

环境配置

在老师给出的pdf作业要求中, 我们需要下载虚拟机并安装Ubuntu, 并在虚拟机中使用VSCode进行编程, 但是我觉得这样太麻烦, 于是我决定在Windows下使用Visual Studio进行编程, 但是由于Eigen库是Linux下的, 所以我需要在Windows下安装Eigen库

Eigen库

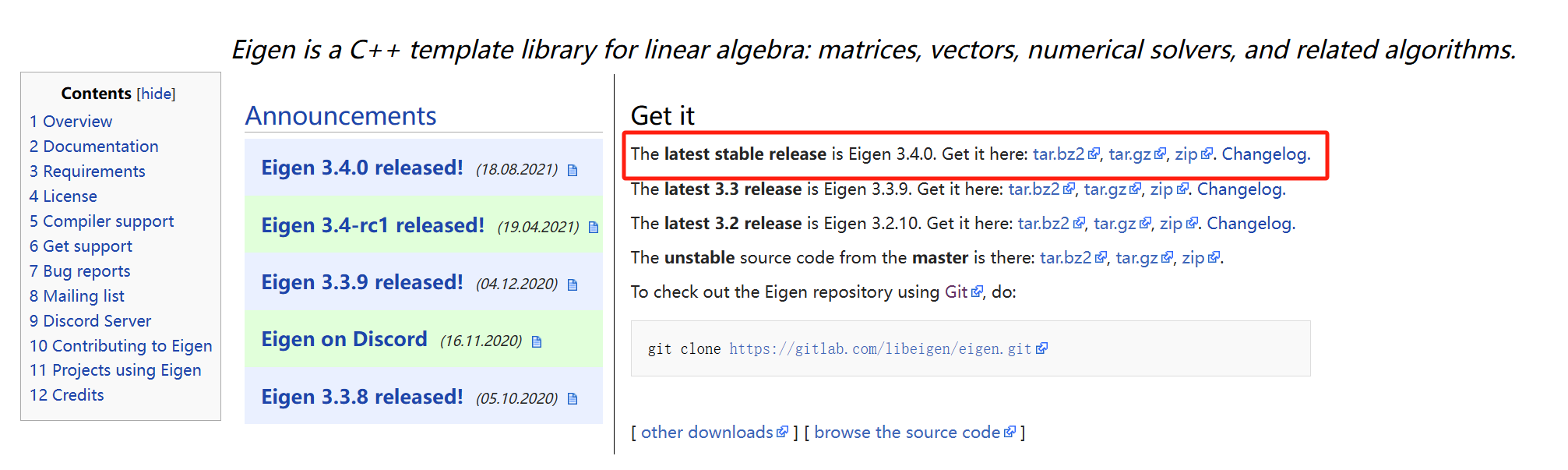
Eigen是一个C++模板库, 提供了线性代数的基本功能, 可以在此网站下载: Eigen

我们选择latest stable release, 下载.zip文件

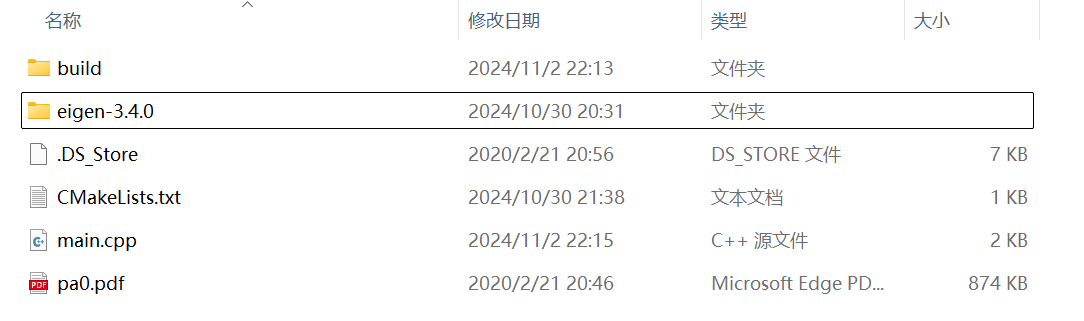
解压后将文件夹放在合适的位置, 我选择放在和作业0文件夹pa0内

由于老师提供的CMakeLists.txt中配置的路径是适用于Linux的, 所以我们需要修改CMakeLists.txt

将以下内容删掉

  
find_package(Eigen3 REQUIRED)
include_directories(EIGEN3_INCLUDE_DIR)

  
include_directories("${CMAKE_SOURCE_DIR}/eigen-3.4.0")

使用CMake生成VS项目

本文默认已经安装了CMake和Visual Studio, 如果没有安装, 请自行安装

在pa0文件夹下新建一个build文件夹, 并在此文件夹中打开cmd, 输入以下命令

cmake ..

等待CMake生成VS项目, 生成成功后, 在build文件夹中会生成一个.sln文件, 双击打开即可

VS配置

在VS中打开项目后, 我们需要配置项目, 以便能够正确运行

首先, 在右侧的解决方案资源管理器中, 右键点击Transformation项目, 选择属性

在VC++目录中, 选择包含目录, 添加之前解压的Eigen的包含目录(注意要加上分号)

F:\Projects\GAMES101-Assignments\pa0\eigen-3.4.0;

不过之前我们已经在CMakeLists.txt中配置了, 所以这里不需要再配置

接着, 在main.cpp中, 我们需要修改include路径

删除原有的:

  
#include<eigen3/Eigen/Core>
#include<eigen3/Eigen/Dense>

改为:

  
#include<Eigen/Core>
#include<Eigen/Dense>

保存即可

编译运行

在VS中, 选择Transformation项目, 右键, 设置为启动项目, 然后按F5编译运行即可

作业内容

已有内容

代码中已经实现了基本的数学运算:

  
 // Basic Example of cpp
 std::cout << "Example of cpp \n";
 float a = 1.0, b = 2.0;
 std::cout << a << std::endl;
 std::cout << a/b << std::endl;
 std::cout << std::sqrt(b) << std::endl;
 std::cout << std::acos(-1) << std::endl;
 std::cout << std::sin(30.0/180.0*acos(-1)) << std::endl;

基本的向量加减及向量与标量相乘:

  
 // Example of vector
 std::cout << "Example of vector \n";
 // vector definition
 Eigen::Vector3f v(1.0f,2.0f,3.0f);
 Eigen::Vector3f w(1.0f,0.0f,0.0f);
 // vector output
 std::cout << "Example of output \n";
 std::cout << v << std::endl;
 // vector add
 std::cout << "Example of add \n";
 std::cout << v + w << std::endl;
 // vector scalar multiply
 std::cout << "Example of scalar multiply \n";
 std::cout << v * 3.0f << std::endl;
 std::cout << 2.0f * v << std::endl;

基本的矩阵输出:

  
 // Example of matrix
 std::cout << "Example of matrix \n";
 // matrix definition
 Eigen::Matrix3f i,j;
 i << 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0;
 j << 2.0, 3.0, 1.0, 4.0, 6.0, 5.0, 9.0, 7.0, 8.0;
 // matrix output
 std::cout << "Example of output \n";
 std::cout << i << std::endl;

作业目标及解决方案

1. 根据数乘的形式与向量点积的形式探索点积的用法

点积的定义是一个向量点乘另一个向量, 得到一个标量, 用于计算两个向量之间的夹角

\[\mathbf{A} \cdot \mathbf{B} = | \mathbf{A} | | \mathbf{B} | \cos \theta = A_x B_x + A_y B_y + A_z B_z\]

其中,

$ \mathbf{A} $ 表示向量, 加上绝对值符号表示向量的模长
$ \theta $ 表示两个向量之间的夹角

  
// 向量点乘及几何意义
Eigen::Vector3f a(1.0f, 2.0f, 3.0f);
Eigen::Vector3f b(0.0f, 1.0f, 2.0f);
std::cout << "a dot b = " << a.dot(b) << std::endl;
std::cout << "|a| = " << a.norm() << std::endl;
std::cout << "|b| = " << b.norm() << std::endl;
std::cout << "cos(a,b) = " << a.dot(b) / (a.norm() * b.norm()) <<std::endl;

2. 探索矩阵加减、数乘、矩阵乘法、矩阵乘向量的用法

矩阵是一个二维数组, 用于表示线性变换:

\[\begin{bmatrix} a & b \\ c & d \end{bmatrix}\]

矩阵与矩阵相加减, 实际上是对应元素相加减:

\[\begin{bmatrix} a & b \\ c & d \end{bmatrix} + \begin{bmatrix} e & f \\ g & h \end{bmatrix} = \begin{bmatrix} a+e & b+f \\ c+g & d+h \end{bmatrix}\]

矩阵与标量相乘, 实际上是矩阵的每个元素与标量相乘:

\[\begin{bmatrix} a & b \\ c & d \end{bmatrix} \times 2 = \begin{bmatrix} 2a & 2b \\ 2c & 2d \end{bmatrix}\]

矩阵乘法, 实际上是矩阵的行乘以另一个矩阵的列:

\[\begin{bmatrix} a & b \\ c & d \end{bmatrix} \times \begin{bmatrix} e & f \\ g & h \end{bmatrix} = \begin{bmatrix} ae+bg & af+bh \\ ce+dg & cf+dh \end{bmatrix}\]

矩阵乘向量, 实际上是矩阵的行乘以向量:

\[\begin{bmatrix} a & b \\ c & d \end{bmatrix} \times \begin{bmatrix} e \\ f \end{bmatrix} = \begin{bmatrix} ae+bf \\ ce+df \end{bmatrix}\]

  
// 矩阵加减、数乘、矩阵乘法、矩阵乘向量
Eigen::Matrix3f m1;
Eigen::Matrix3f m2;
m1 << 1, 2, 3, 4, 5, 6, 7, 8, 9;
m2 << 1, 0, 0, 0, 1, 0, 0, 0, 1;
std::cout << "m1 + m2 = \n" << m1 + m2 << std::endl;
std::cout << "m1 - m2 = \n" << m1 - m2 << std::endl;
std::cout << "m1 * 2 = \n" << m1 * 2 << std::endl;
std::cout << "m1 * m2 = \n" << m1 * m2 << std::endl;
Eigen::Vector3f v1(1.0f, 2.0f, 3.0f);
std::cout << "m1 * v1 = \n" << m1 * v1 << std::endl;

3. 点的旋转, 平移

给定一个点P=(2,1),将该点绕原点先逆时针旋转45◦，再平移(1,2),计算出变换后点的坐标(要求用齐次坐标进行计算)

齐次坐标是一种将点的坐标和向量的坐标统一起来的方法, 通过增加一个维度, 将点和向量统一为一个4维向量, 通过矩阵乘法, 可以实现旋转, 平移等操作

例如: 如果一个点P=(x, y), 通过齐次坐标, 可以表示为P=(x, y, 1), 如果一个向量V=(x, y), 通过齐次坐标, 可以表示为V=(x, y, 0)

我们先声明一个点的齐次坐标:

  
Eigen::Vector3f p(2.0f, 1.0f, 1.0f);

要求绕原点逆时针旋转45°, 我们可以声明旋转矩阵, 注意, 原本旋转矩阵是一个二维矩阵:

\[\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}\]

但是由于点使用了齐次坐标, 所以旋转矩阵也需要使用齐次坐标:

\[\begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix}\]

其中, $\theta = 45° = \frac{\pi}{4}$

注意, 如果要求不是绕着原点旋转, 而是绕着其他点旋转, 需要先平移, 再旋转, 再平移回来

例如, 要让点(x, y)绕点(a, b)旋转45°:

平移到原点: (x, y)移动为(x-a, y-b)
旋转45°: 旋转矩阵R(45°)作用在(x-a, y-b)上
平移回去: 将旋转后的点(x', y')平移回去, 得到最终点(x', y') + (a, b)

数学表达式为:

\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a \\ b \end{bmatrix} + R(45°) \times \begin{bmatrix} x-a \\ y-b \end{bmatrix}\]

回到问题, 我们声明旋转矩阵:

  
Eigen::Matrix3f r;
r << cos(M_PI/4), -sin(M_PI/4), 0, sin(M_PI/4), cos(M_PI/4), 0, 0, 0, 1;

但是M_PI是Linux下的宏定义, Windows下没有, 所以我们需要自己定义:

#define M_PI 3.14159265358979323846

平移矩阵用于将点平移到新的位置上去, 普通的平移操作不能用常规的2D矩阵表示, 因为平移操作是一个向量加法:

\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} x + a \\ y + b \end{bmatrix}\]

这里的平移量是

\[\begin{bmatrix} a \\ b \end{bmatrix}\]

如果我们需要用矩阵表示平移, 则需要将其扩展成齐次坐标的形式:

\[\begin{bmatrix} 1 & 0 & a \\ 0 & 1 & b \\ 0 & 0 & 1 \end{bmatrix}\]

平移点则将此矩阵作用在点上:

\[\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & a \\ 0 & 1 & b \\ 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} x + a \\ y + b \\ 1 \end{bmatrix}\]

现在我们声明平移矩阵:

  
Eigen::Matrix3f t;
t << 1, 0, 1, 0, 1, 2, 0, 0, 1;

最后, 我们将旋转矩阵和平移矩阵作用在点上:

  
std::cout << "p = \n" << p << std::endl;
std::cout << "r = \n" << r << std::endl;
std::cout << "t = \n" << t << std::endl;
std::cout << "t * r * p = \n" << t * r * p << std::endl;

顺序很重要, 一般来说, 先旋转, 再平移

完整代码

  
#include<cmath>
#include<Eigen/Core>
#include<Eigen/Dense>
#include<iostream>

#define M_PI 3.14159265358979323846

int main(){  
    // 向量点乘及几何意义
    Eigen::Vector3f a(1.0f, 2.0f, 3.0f);
    Eigen::Vector3f b(0.0f, 1.0f, 2.0f);
    std::cout << "a dot b = " << a.dot(b) << std::endl;
    std::cout << "|a| = " << a.norm() << std::endl;
    std::cout << "|b| = " << b.norm() << std::endl;
    std::cout << "cos(a,b) = " << a.dot(b) / (a.norm() * b.norm()) << std::endl;
        
    std::cout << "\n";
    
    // 矩阵加减、数乘、矩阵乘法、矩阵乘向量
    Eigen::Matrix3f m1;
    Eigen::Matrix3f m2;
    m1 << 1, 2, 3, 4, 5, 6, 7, 8, 9;
    m2 << 1, 0, 0, 0, 1, 0, 0, 0, 1;
    Eigen::Vector3f v1(1.0f, 2.0f, 3.0f);
    std::cout << "m1 = \n" << m1 << std::endl;
    std::cout << "m2 = \n" << m2 << std::endl;
    std::cout << "v1 = \n" << v1 << std::endl;
    std::cout << "m1 + m2 = \n" << m1 + m2 << std::endl;
    std::cout << "m1 - m2 = \n" << m1 - m2 << std::endl;
    std::cout << "m1 * 2 = \n" << m1 * 2 << std::endl;
    std::cout << "m1 * m2 = \n" << m1 * m2 << std::endl;
    std::cout << "m1 * v1 = \n" << m1 * v1 << std::endl;
    
    std::cout << "\n";
    
    // 点的旋转, 平移
    // 给定一个点`P=(2,1)`,将该点绕原点先逆时针旋转`45◦`，再平移`(1,2)`,计算出变换后点的坐标(要求用 齐次坐标进行计算)
    // 定义点P
    Eigen::Vector3f p(2.0f, 1.0f, 1.0f);
    // 旋转矩阵
    Eigen::Matrix3f r;
    r << cos(M_PI / 4), -sin(M_PI / 4), 0, sin(M_PI / 4), cos(M_PI / 4), 0, 0, 0, 1;
    // 平移矩阵
    Eigen::Matrix3f t;
    t << 1, 0, 1, 0, 1, 2, 0, 0, 1;
    // 计算变换后的点
    std::cout << "p = \n" << p << std::endl;
    std::cout << "r = \n" << r << std::endl;
    std::cout << "t = \n" << t << std::endl;
    std::cout << "t * r * p = \n" << t * r * p << std::endl;
    
    return 0;
}

笔记, GAMES101

本文由作者按照 CC BY 4.0 进行授权