GAMES101 第2讲线性代数

发表于 2024/11/10

作者 Wang Simiao

10 分钟阅读

GAMES101 第2讲线性代数

向量

向量的定义

写作
- 箭头表示: $\vec{a}$
- 粗体表示: $\mathbf{a}$
基于起点与终点: $\vec{AB} = B - A$
最重要的属性:
- 长度
- 方向
没有绝对的起点和终点(平移不变性)

向量的单位化

向量的长度大小通常写成 $ \vec{a} $
单位化后的向量记作 $ \hat{a} $

\[\hat{a} = \frac{\vec{a}}{||\vec{a}||}\]

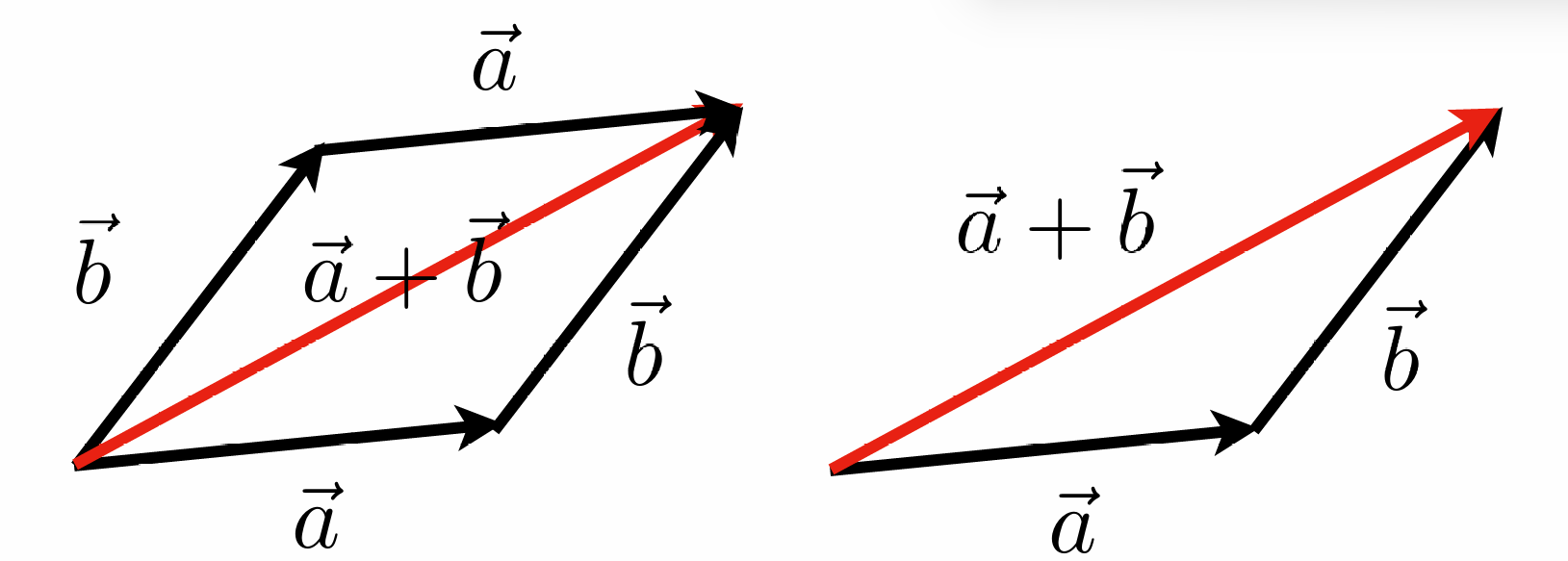
向量求和

几何: 平行四边形法则/三角形法则
代数: 坐标直接相加

笛卡尔坐标系

笛卡尔坐标系: 以直角为基础的坐标系, 通常用于表示二维或三维空间中的点或向量

在二维坐标系中, 任何一个向量都可以表示为两个基向量的线性组合

\[A = \begin{bmatrix} x \\ y \end{bmatrix}\]

$A^T$ 表示 $A$ 的转置, 即将 $A$ 的行向量转换为列向量

\[A^T = \begin{bmatrix} x & y \end{bmatrix}\]

在笛卡尔二维坐标系中, 向量$A$的长度可以表示为:

\[||A|| = \sqrt{x^2 + y^2}\]

向量的点乘

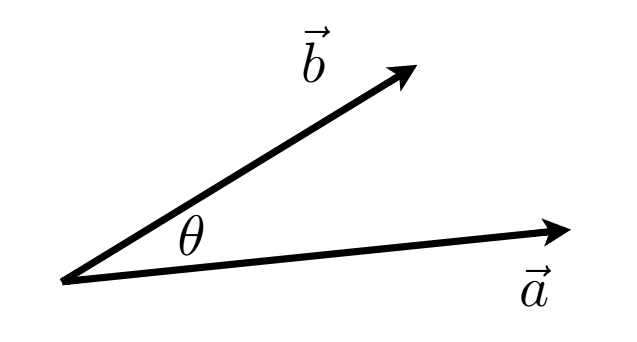
在几何上的理解

向量的点乘的标准定义:

\[\vec{a} \cdot \vec{b} = ||\vec{a}|| \cdot ||\vec{b}|| \cdot \cos(\theta)\]

由此可得:

\[\cos(\theta) = \frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| \cdot ||\vec{b}||}\]

对于单位向量, 它们点乘即为夹角的余弦值:

\[\cos(\theta) = \hat{a} \cdot \hat{b}\]

点乘的性质:

交换律: $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$
分配律: $\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}$
乘法结合律: $(k\vec{a}) \cdot \vec{b} = k(\vec{a} \cdot \vec{b}) = \vec{a} \cdot (k\vec{b})$

迪卡尔坐标系下的点乘

2D 点乘:

\[\vec{a} \cdot \vec{b} = \begin{bmatrix} x_a \\ y_a \end{bmatrix} \cdot \begin{bmatrix} x_b \\ y_b \end{bmatrix} = x_a \cdot x_b + y_a \cdot y_b\]

3D 点乘:

\[\vec{a} \cdot \vec{b} = \begin{bmatrix} x_a \\ y_a \\ z_a \end{bmatrix} \cdot \begin{bmatrix} x_b \\ y_b \\ z_b \end{bmatrix} = x_a \cdot x_b + y_a \cdot y_b + z_a \cdot z_b\]

图形学中的应用

找到两个向量之间的夹角(判断是否垂直)
找到一个向量在另一个向量上的投影(投影长度)

向量的叉乘

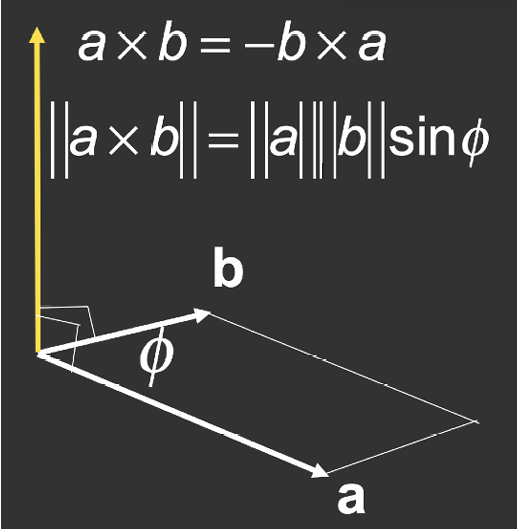
基本概念

\[\vec{a} \times \vec{b} = -\vec{b} \times \vec{a}\] \[||\vec{a} \times \vec{b}|| = ||\vec{a}|| \cdot ||\vec{b}|| \cdot \sin(\theta)\]

法向量: 向量叉乘得到的向量与两个初始向量都垂直(垂直于两个向量所在的平面)
遵循右手定则: 四根手指从第一个向量转向第二个向量, 大拇指指向叉乘结果
不满足交换律: $\vec{a} \times \vec{b} \neq \vec{b} \times \vec{a}$
对构造坐标系有很大的帮助

在三维笛卡尔坐标系下的叉乘

叉乘可用于构造三维笛卡尔坐标系, 只需要两个向量即可构造出第三个向量

\[\vec{x} \times \vec{y} = + \vec{z} \\ \vec{y} \times \vec{x} = - \vec{z} \\ \vec{y} \times \vec{z} = + \vec{x} \\ \vec{z} \times \vec{y} = - \vec{x} \\ \vec{z} \times \vec{x} = + \vec{y} \\ \vec{x} \times \vec{z} = - \vec{y}\]

叉乘的基本数学性质

叉乘不满足交换律, 但满足以下性质:

\[\begin{align} \vec{a} \times \vec{b} = - \vec{b} \times \vec{a} \\ \vec{a} \times \vec{a} = \vec{0} \\ \vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c} \\ (k\vec{a}) \times \vec{b} = k(\vec{a} \times \vec{b}) = \vec{a} \times (k\vec{b}) \end{align}\]

叉乘在代数上的表示

在三维笛卡尔坐标系下, 叉乘的计算公式为:

\[\vec{a} \times \vec{b} = \begin{bmatrix} y_a \cdot z_b - y_b \cdot z_a \\ z_a \cdot x_b - x_a \cdot z_b \\ x_a \cdot y_b - y_a \cdot x_b \end{bmatrix}\]

向量的叉乘可以表示成矩阵的形式: 即向量$\vec{a}$可以写成矩阵$\mathbf{A}$

\[\vec{a} \times \vec{b} = \mathbf{A}^{*} \vec{b} = \begin{bmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0 \end{bmatrix} \begin{bmatrix} x_b \\ y_b \\ z_b \end{bmatrix}\]

向量的叉乘在图形学中的应用

判定左和右: 例如, 在屏幕上, 向量$\vec{a}$和向量$\vec{b}$的叉乘结果的$z$分量的正负可以判断$\vec{a}$在$\vec{b}$的左边还是右边

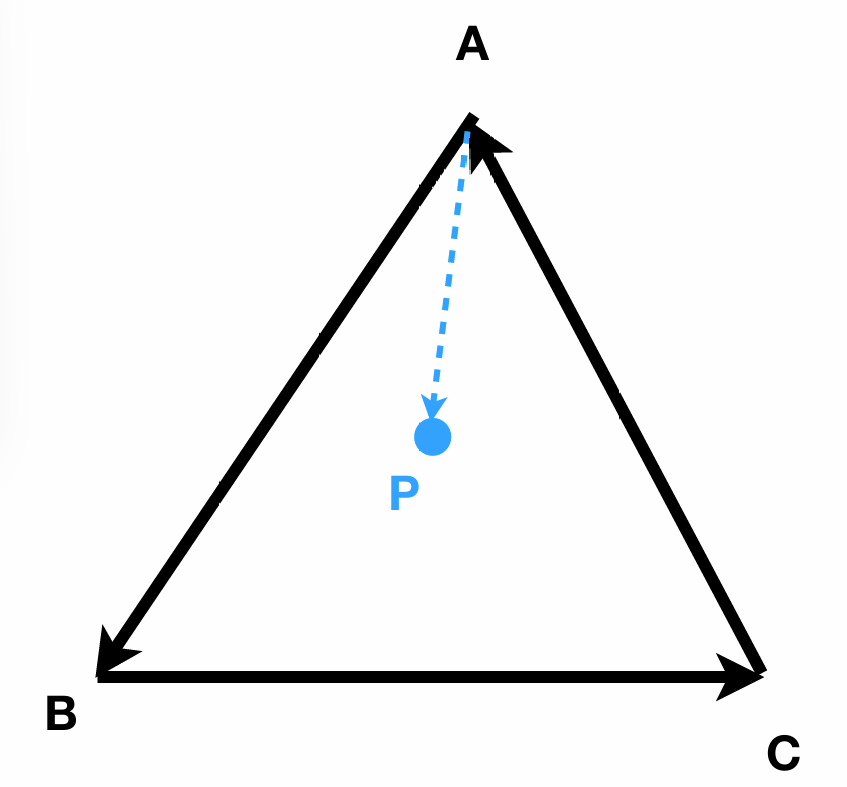
判定内和外: 例如在三角型中, 要判断点P是否在三角形ABC内部, 可以通过向量$\vec{AB}$和向量$\vec{AP}$的叉乘结果的$z$分量的正负来判断

三维正交坐标系

给定三个向量满足以下条件:

\[|| \vec{u} || = || \vec{v} || = || \vec{w} || = 1 \\ \vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{u} = 0 \vec{w} = \vec{u} \times \vec{v}\]

则任意一个向量$\vec{p}$都可以表示为:

\[\vec{p} = (\vec{p} \cdot \vec{u}) \vec{u} + (\vec{p} \cdot \vec{v}) \vec{v} + (\vec{p} \cdot \vec{w}) \vec{w}\]

这里的$\vec{p} \cdot \vec{u}$, $\vec{p} \cdot \vec{v}$, $\vec{p} \cdot \vec{w}$分别表示$\vec{p}$在$\vec{u}$, $\vec{v}$, $\vec{w}$上的投影

矩阵

矩阵的定义

矩阵是一个二维数组($m \times n$, $m$行$n$列), 通常用大写字母表示

矩阵的运算

矩阵与标量的数学运算

矩阵与标量的加法:

\[x + \begin{bmatrix} a & b \\ c & d \end{bmatrix}= \begin{bmatrix} x + a & x + b \\ x + c & x + d \end{bmatrix}\]

矩阵与标量的乘法:

\[x \cdot \begin{bmatrix} a & b \\ c & d \end{bmatrix}= \begin{bmatrix} x \cdot a & x \cdot b \\ x \cdot c & x \cdot d \end{bmatrix}\]

矩阵与矩阵的乘积(重要)

前提: 第一个矩阵的列数等于第二个矩阵的行数

结果: $(M \times N) \times (N \times P) = M \times P$

例如下方的矩阵相乘, 第一个矩阵是3行2列, 第二个矩阵是2行3列, 第一个矩阵的列数等于第二个矩阵的行数, 因此可以相乘, 结果是3行3列的矩阵

\[\begin{bmatrix} a & b \\ c & d \\ e & f \end{bmatrix} \begin{bmatrix} x & y & z \\ u & v & w \end{bmatrix}= \begin{bmatrix} a \cdot x + b \cdot u & a \cdot y + b \cdot v & a \cdot z + b \cdot w \\ c \cdot x + d \cdot u & c \cdot y + d \cdot v & c \cdot z + d \cdot w \\ e \cdot x + f \cdot u & e \cdot y + f \cdot v & e \cdot z + f \cdot w \end{bmatrix}\]

计算方法: 如果我们想找结果矩阵的第$i$行第$j$列的元素, 可以将第一个矩阵的第$i$行和第二个矩阵的第$j$列对应元素相乘, 然后相加, 即:

\[C_{ij} = \sum_{k=1}^{N} A_{ik} \cdot B_{kj}\]

性质 :

没有任何交换律: $AB \neq BA$
结合律: $(AB)C = A(BC)$
分配律: 注意前后顺序不能颠倒
- $A(B + C) = AB + AC$
- $(A + B)C = AC + BC$

矩阵与向量相乘

将向量视为一个 $m \times 1 $ 的列矩阵(即是竖着的, 列数为1的矩阵)

例如: 将一个向量沿y轴轴对称变换

\[\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} -x \\ y \end{bmatrix}\]

矩阵的转置

矩阵的转置是将矩阵的行和列互换得到的新矩阵, 记作$A^T$

例如:

\[\begin{bmatrix} a & b \\ c & d \\ e & f \end{bmatrix}^T = \begin{bmatrix} a & c & e \\ b & d & f \end{bmatrix}\]

性质: 如果对两个相乘的矩阵取转置, 结果是后一个矩阵的转置与前一个矩阵的转置相乘

\[(AB)^T = B^T A^T\]

单位矩阵

单位矩阵是一个对角线上的元素都是1, 其他元素都是0的矩阵, 且行数等于列数, 记作$I$

\[I_{3 \times 3} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]

矩阵的逆

逆矩阵: 一个矩阵与其逆矩阵相乘必定得到单位矩阵, 记作$A^{-1}$

性质:

$A A^{-1} = A^{-1} A = I$
$(AB)^{-1} = B^{-1} A^{-1}$

向量以矩阵的形式表示

点乘

\[\vec{a} \cdot \vec{b} = \vec{a}^T \vec{b} = \begin{bmatrix} x_a & y_a & z_a \end{bmatrix} \begin{bmatrix} x_b \\ y_b \\ z_b \end{bmatrix} = x_a \cdot x_b + y_a \cdot y_b + z_a \cdot z_b\]

叉乘