GAMES101 第3讲 变换(二维)
二维空间中的变换
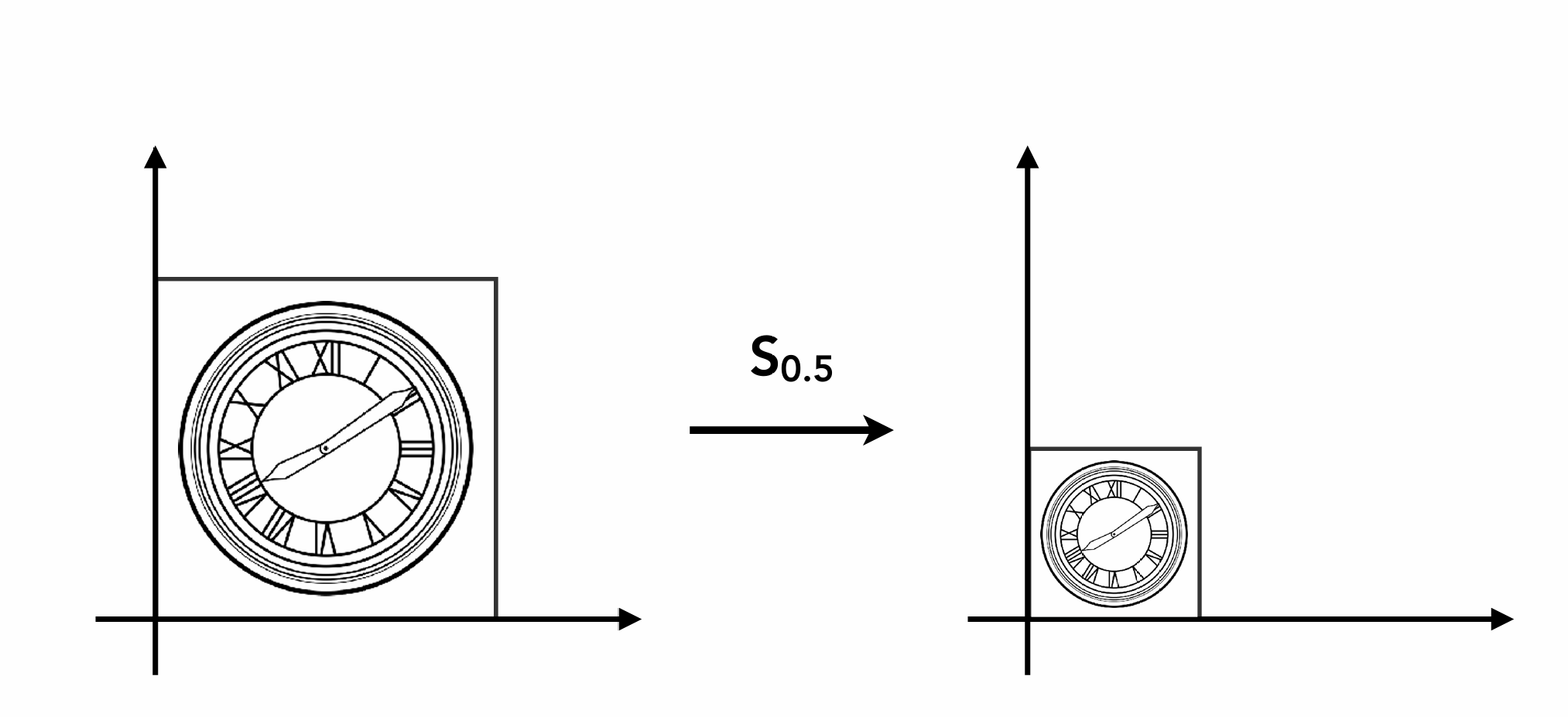
缩放
坐标经过缩放后, 坐标的变化为:
\[x' = s \cdot x\] \[y' = s \cdot y\]其中 $s$ 的值为 $ 0.5 $ , 表示缩小一半。
可以写成矩阵的形式:
\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]缩放矩阵可以写成一个对角矩阵, 对角线上的元素为缩放的比例
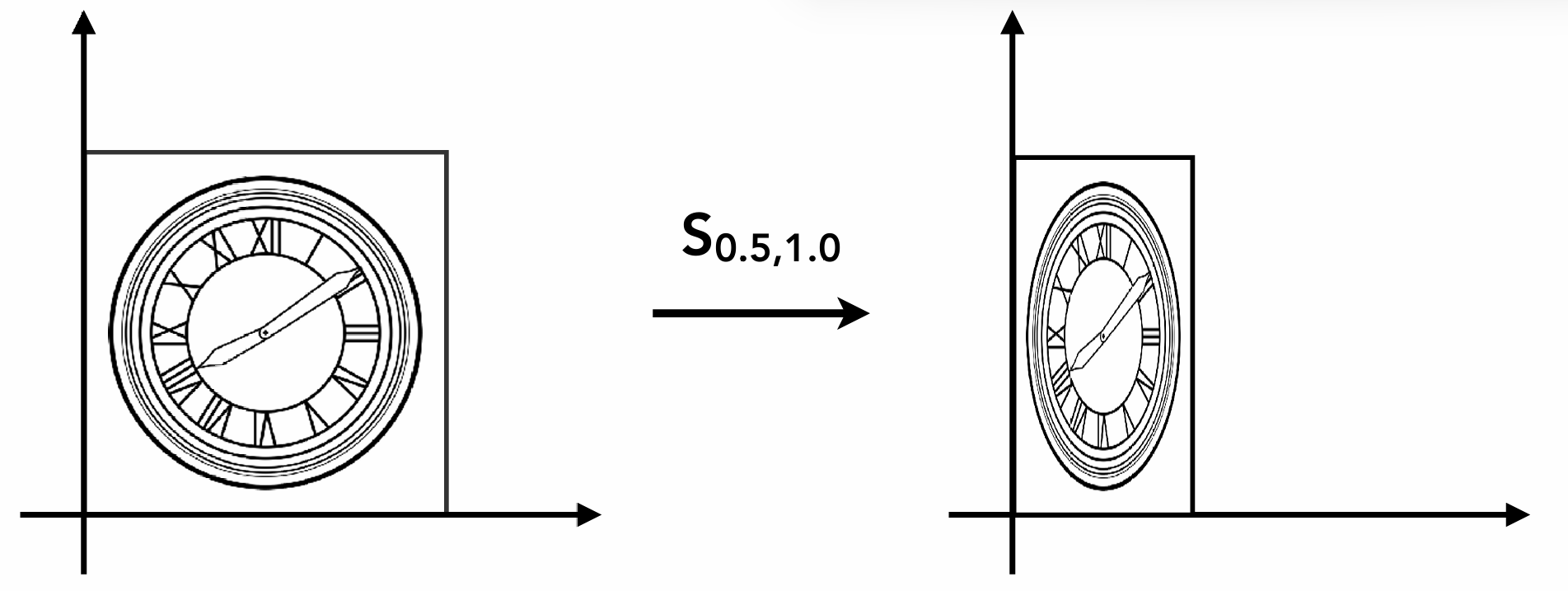
当x与y轴缩放比例不相等时, 可以写成:
\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]对称(反射)
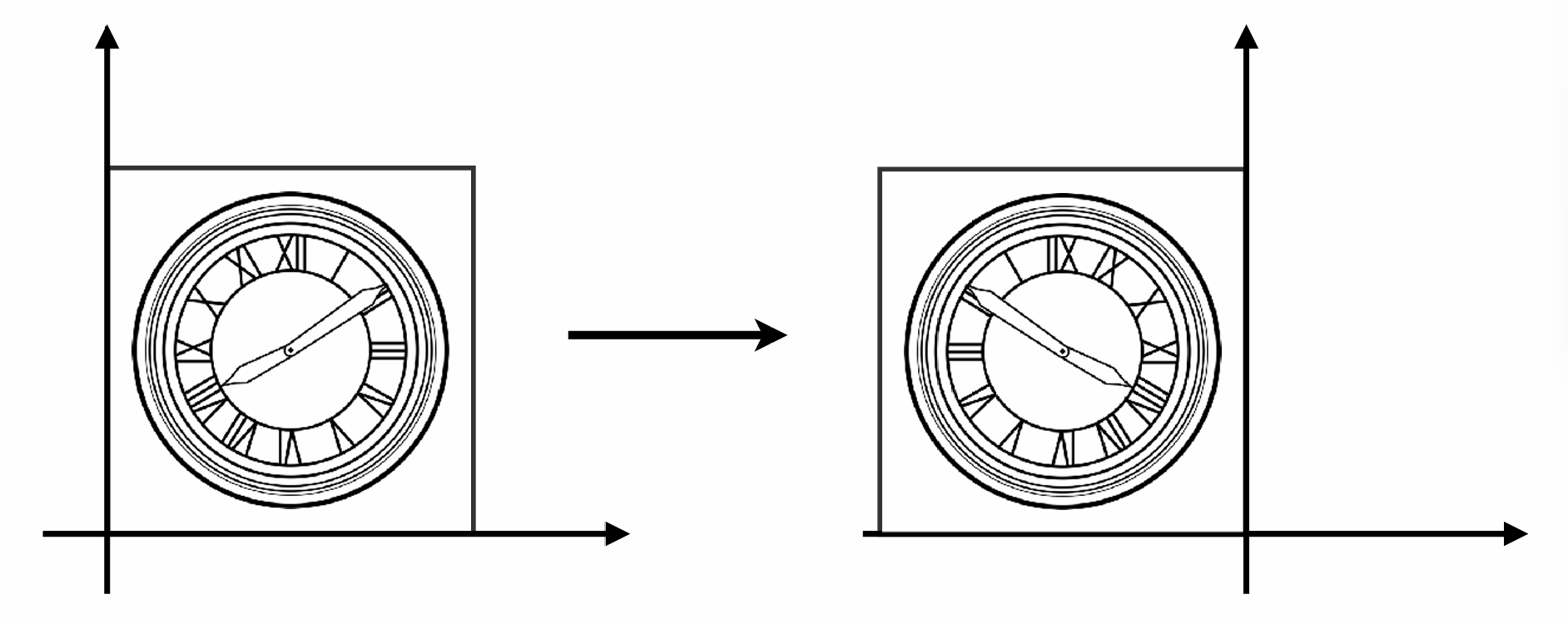
对称变换是一种特殊的缩放变换, 缩放比例为 $-1$, 在图中的情况下:
\[x' = -x \\ y' = y\]可以写成矩阵的形式:
\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]切变
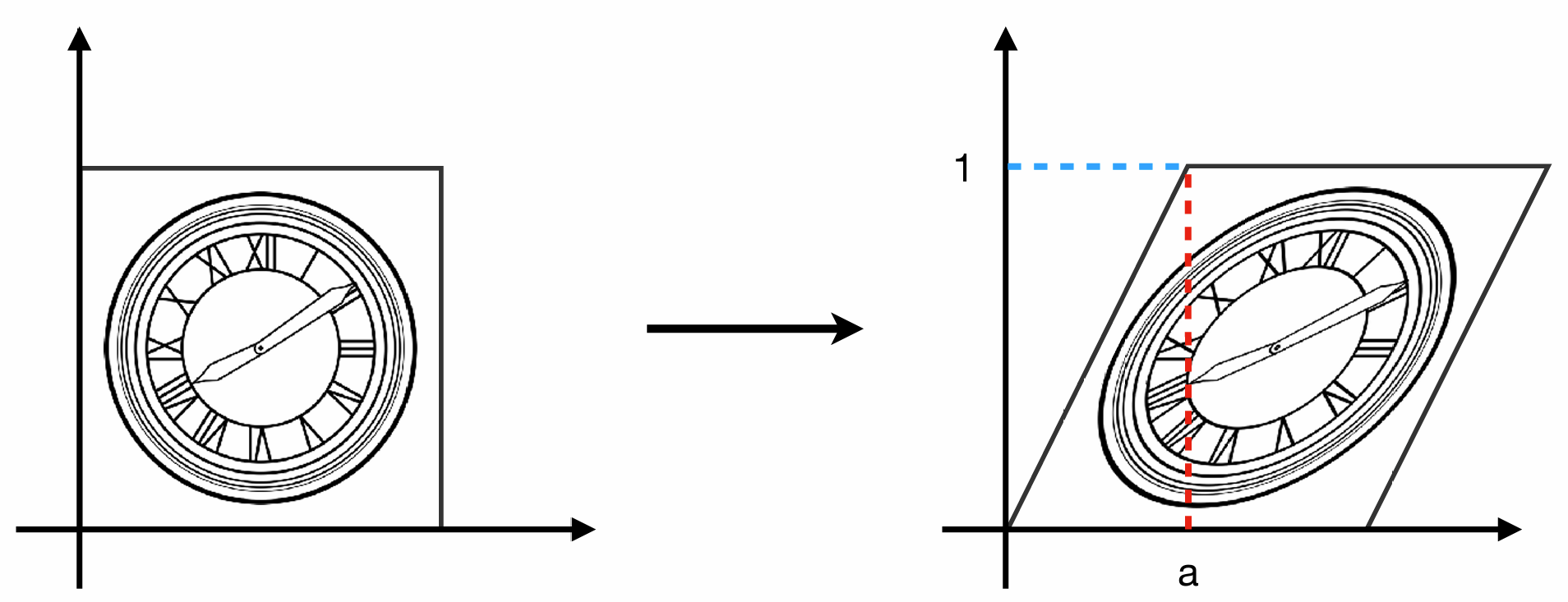
在图中的情况下, 任意一个点的 $y$ 坐标没有变化, $x$ 坐标的变化为:
- 当 $y = 0$ 时, $x’ = x$
- 当 $y = 1$ 时, $x’ = x + a$
也就是说, x坐标的变化量为 $a \cdot y$, 以矩阵的形式表示为:
\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]旋转
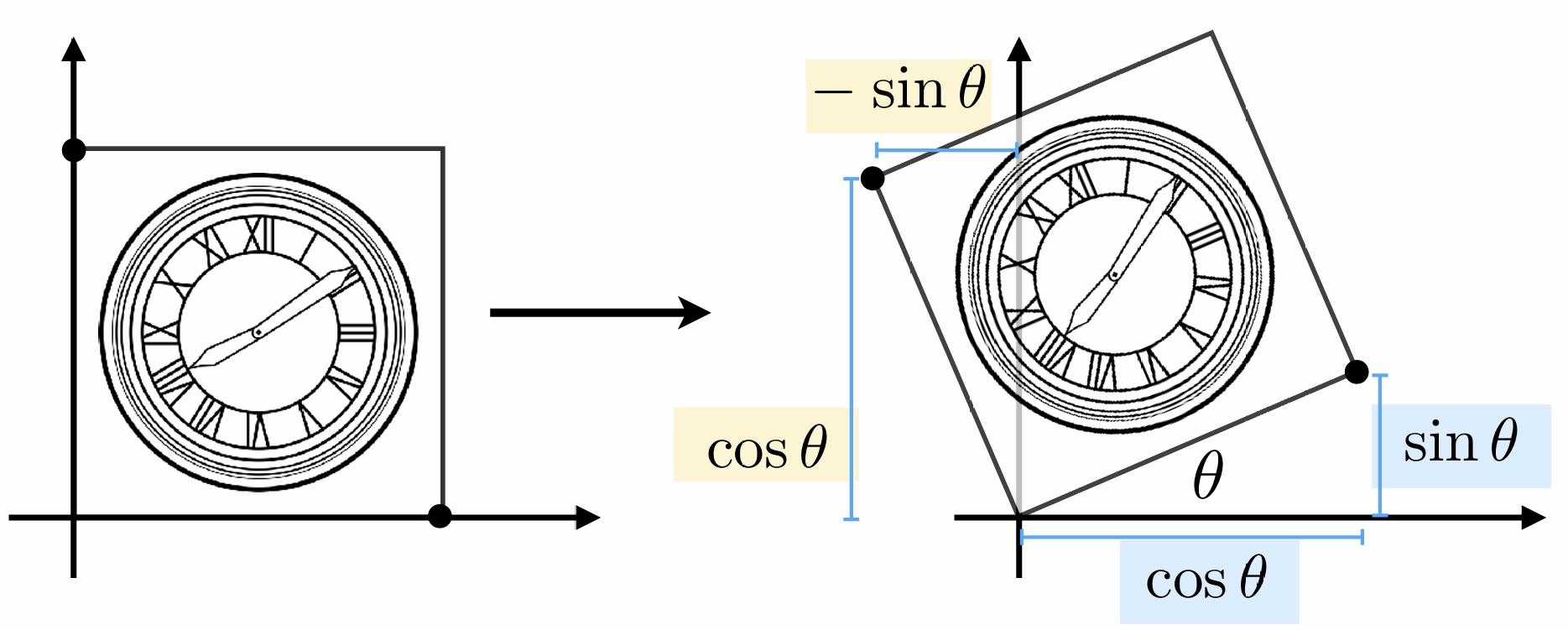
任何旋转我们都默认为绕着原点 $(0, 0)$ 旋转, 默认的旋转方向为逆时针方向
二维旋转矩阵为:
\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]二维旋转矩阵的推导
假设一个点 $(x, y)$ 绕原点 $(0, 0)$ 逆时针旋转 $\theta$ 角度后的坐标为 $(x’, y’)$
\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} ? & ? \\ ? & ? \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]当该点原坐标 $(x, y)$ 为 $(1, 0)$ 时, 旋转后的坐标 $(x’, y’)$ 为 $(cos(\theta), sin(\theta))$
\[\begin{bmatrix} cos(\theta) \\ sin(\theta) \end{bmatrix} = \begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix}\]解方程得到:
\[cos(\theta) = A \cdot 1 + B \cdot 0 = A\] \[sin(\theta) = C \cdot 1 + D \cdot 0 = C\]同理, 当该点原坐标 $(x, y)$ 为 $(0, 1)$ 时, 旋转后的坐标 $(x’, y’)$ 为 $(-sin(\theta), cos(\theta))$
\[\begin{bmatrix} -sin(\theta) \\ cos(\theta) \end{bmatrix} = \begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix}\]解方程得到:
\[-sin(\theta) = A \cdot 0 + B \cdot 1 = B\] \[cos(\theta) = C \cdot 0 + D \cdot 1 = D\]综上所述, 二维旋转矩阵为:
\[\begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix}\]相反方向的旋转矩阵
如果要旋转 $ -\theta $ 角度, 则旋转矩阵的推导过程为:
\[R_{-\theta} = \begin{bmatrix} cos(-\theta) & -sin(-\theta) \\ sin(-\theta) & cos(-\theta) \end{bmatrix}= \begin{bmatrix} cos(\theta) & sin(\theta) \\ -sin(\theta) & cos(\theta) \end{bmatrix} = R_{\theta}^{T}\]同时, 从定义上看, 旋转 $ -\theta $ 角与旋转 $ \theta $ 角正好应该是互逆的操作, 即向相反方向旋转的矩阵等于旋转矩阵的逆矩阵:
\[R_{-\theta} = R_{\theta}^{-1}\]因此, 在旋转的矩阵中, 旋转矩阵的逆矩阵就是其转置矩阵
\[R_{-\theta} = R_{\theta}^{-1} = R_{\theta}^{T}\]如果一个矩阵的逆矩阵等于其转置矩阵, 则称这个矩阵为正交矩阵
线性变换
当一个变换可以写成以下形式时, 称为线性变换:
\[x' = a \cdot x + b \cdot y\] \[y' = c \cdot x + d \cdot y\]也就是说, 如果一个变换可以写成矩阵的形式:
\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]即若 $x’ = \mathbf{M}x$ ,则称这个变换为线性变换
齐次坐标
引入齐次坐标的原因
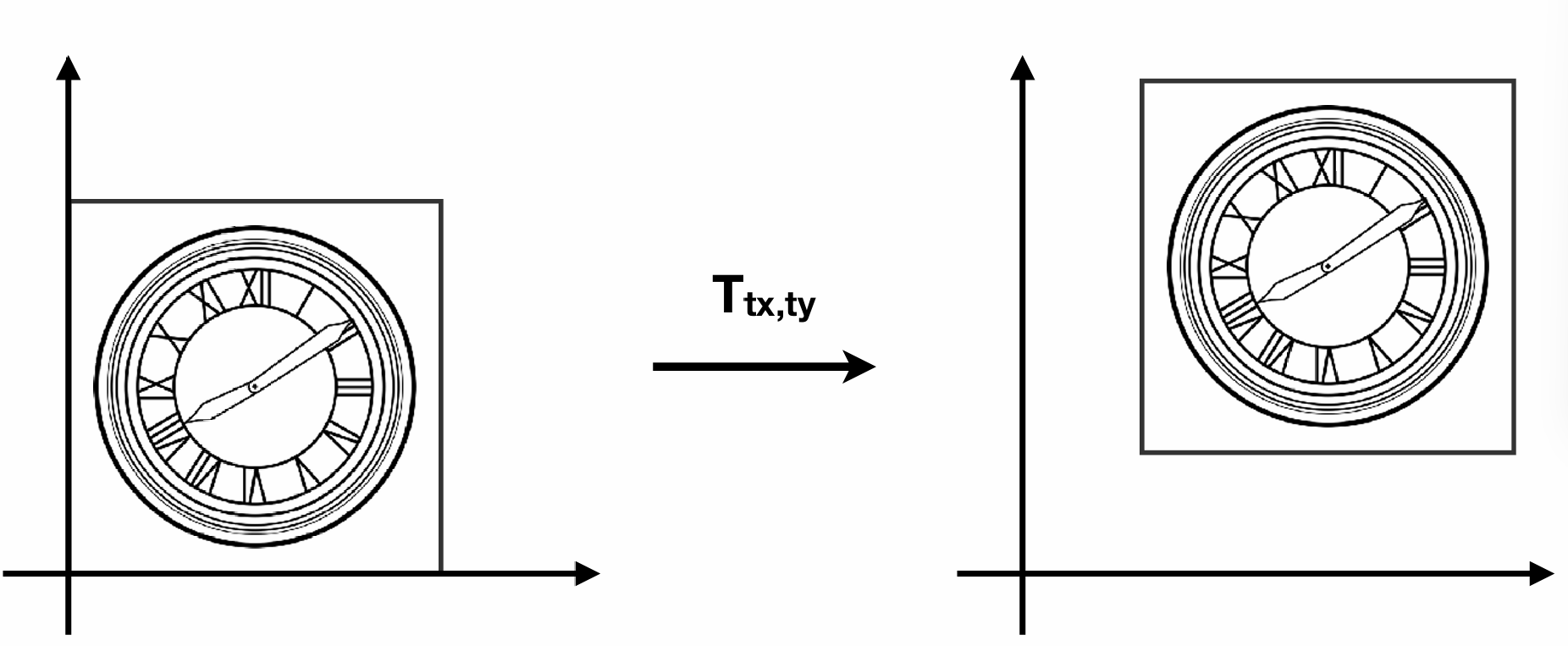
平移变换是一种比较特殊的变换, 无法用线性变换的形式表示, 但是可以用齐次坐标的形式表示
\[x' = x + t_x\] \[y' = y + t_y\]只能写作以下形式:
\[\begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix}\]所以, 平移变换不是线性变换
但是, 我们不想要这样的结果, 我们希望所有的变换都可以写成线性变换的形式, 所以引入了齐次坐标 (当然, 这是有代价的: No Free Lunch)
齐次坐标
引入一个新的形式来表示坐标变换: 增加一个维度
- 2D的点: $(x, y, 1)^T$
- 2D的向量: $(x, y, 0)^T$
矩阵的形式表示平移变换:
\[\begin{bmatrix} x' \\ y' \\ w' \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} x + t_x \\ y + t_y \\ 1 \end{bmatrix}\]向量的齐次坐标最后一位是0, 在平移的矩阵乘法中不会影响结果, 体现了向量的平移不变性
- 向量 + 向量 = 向量
- 点 - 点 = 向量
- 点 + 向量 = 点
- 点 + 点 = 无意义
在二维齐次坐标中, 一个点的坐标$(x/w, y/w)$可以表示为:
\[\begin{bmatrix} x \\ y \\ w \end{bmatrix} = \begin{bmatrix} x/w \\ y/w \\ 1 \end{bmatrix} , w \neq 0\]推论: 在齐次坐标中, 一个点加一个点的结果是两个点的中点
\[\begin{bmatrix} x_1 \\ y_1 \\ w_1 \end{bmatrix} + \begin{bmatrix} x_2 \\ y_2 \\ w_2 \end{bmatrix} = \begin{bmatrix} x_1/w_1 \\ y_1/w_1 \\ 1 \end{bmatrix} + \begin{bmatrix} x_2/w_2 \\ y_2/w_2 \\ 1 \end{bmatrix} = \begin{bmatrix} (x_1/w_1 + x_2/w_2) \\ (y_1/w_1 + y_2/w_2) \\ 2 \end{bmatrix}\] \[\begin{bmatrix} (x_1/w_1 + x_2/w_2) \\ (y_1/w_1 + y_2/w_2) \\ 2 \end{bmatrix} = \begin{bmatrix} (x_1/w_1 + x_2/w_2) / 2 \\ (y_1/w_1 + y_2/w_2) / 2 \\ 1 \end{bmatrix}\]所有变换的齐次坐标形式
对于任何一种变换(无论是线性变换还是非线性变换), 只要满足以下形式:
\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix}\]都称其为仿射变换(Affine Transformation)
仿射变换的齐次坐标形式为:
\[\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}\]其中, $ a, b, c, d $ 为线性变换的矩阵参数, $ t_x, t_y $ 为平移的矩阵参数
缩放, 旋转, 平移的齐次坐标矩阵
缩放
\[S_{(s_x, s_y)} = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix}\]旋转
\[R_{\theta} = \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix}\]平移
\[T_{(t_x, t_y)} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix}\]逆变换
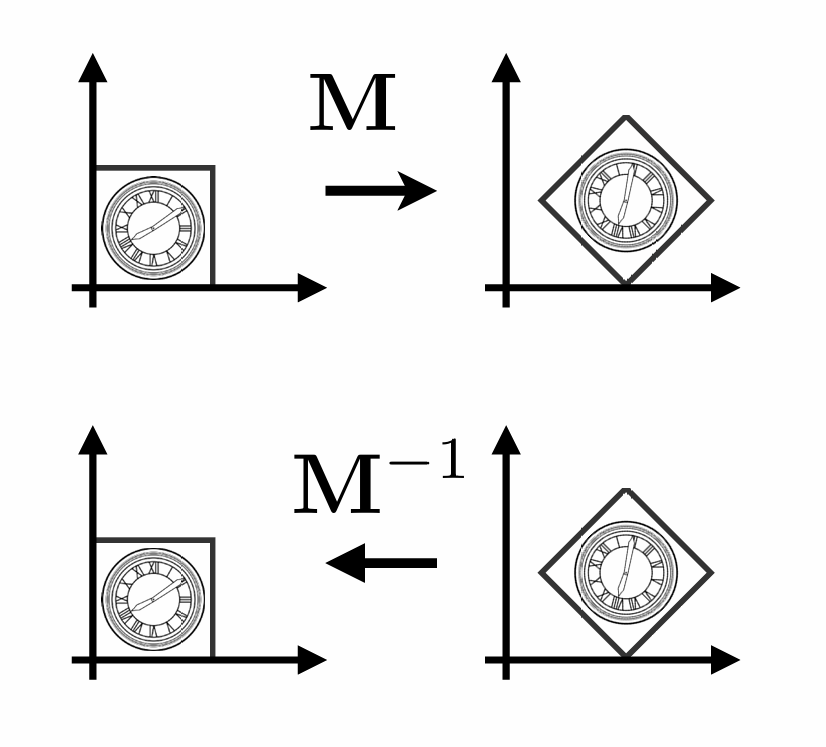
将一个变换的操作逆转, 称为逆变换
在数学上, 逆变换的矩阵为原变换矩阵的逆矩阵
变换的组合
变换的顺序
变换的组合是指将多个变换按照一定的顺序进行组合, 使得多个变换的效果等同于一个变换
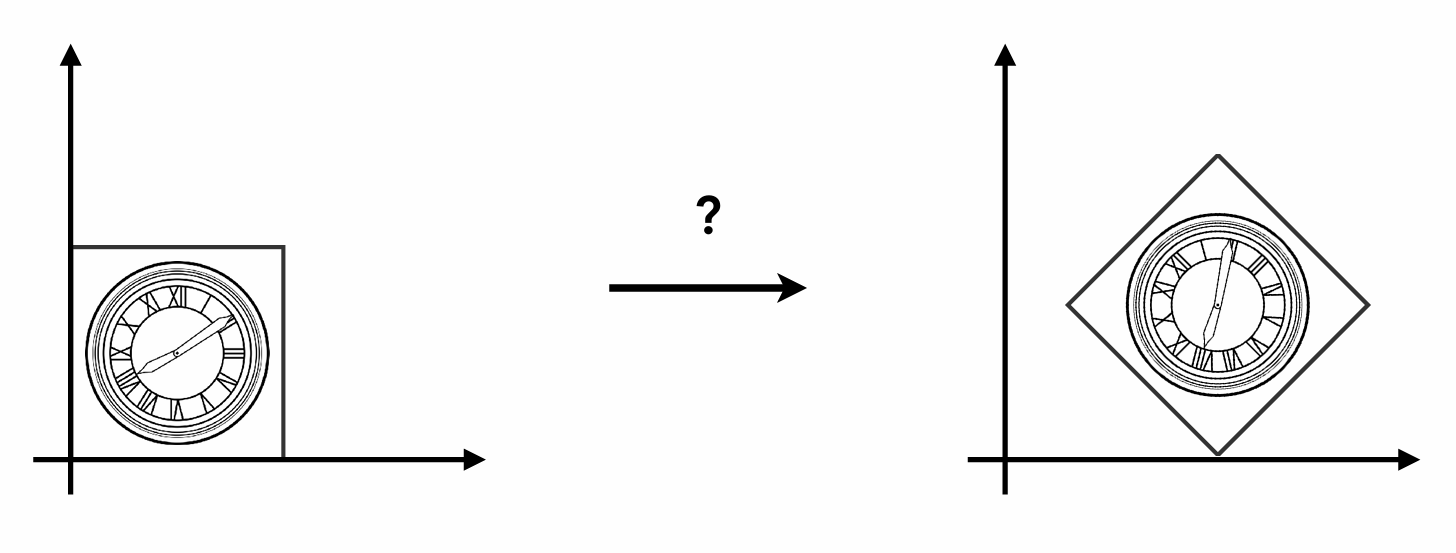
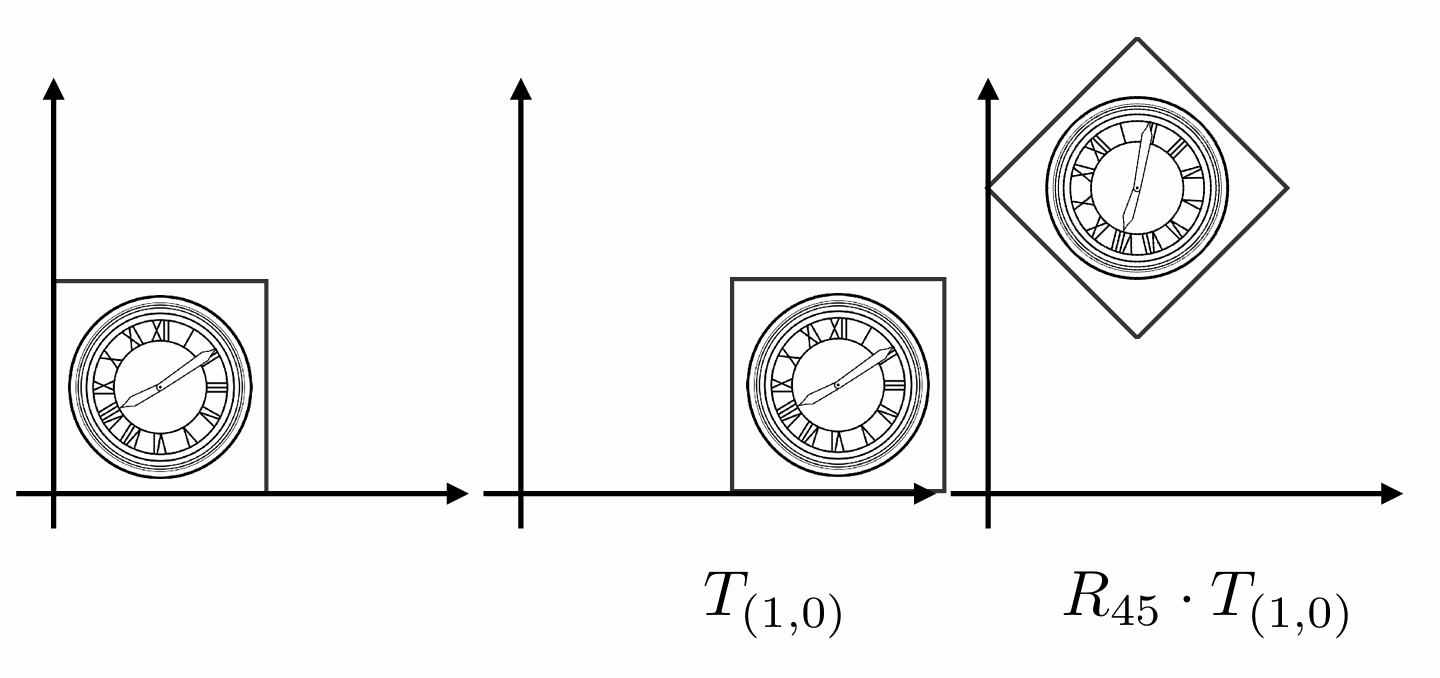
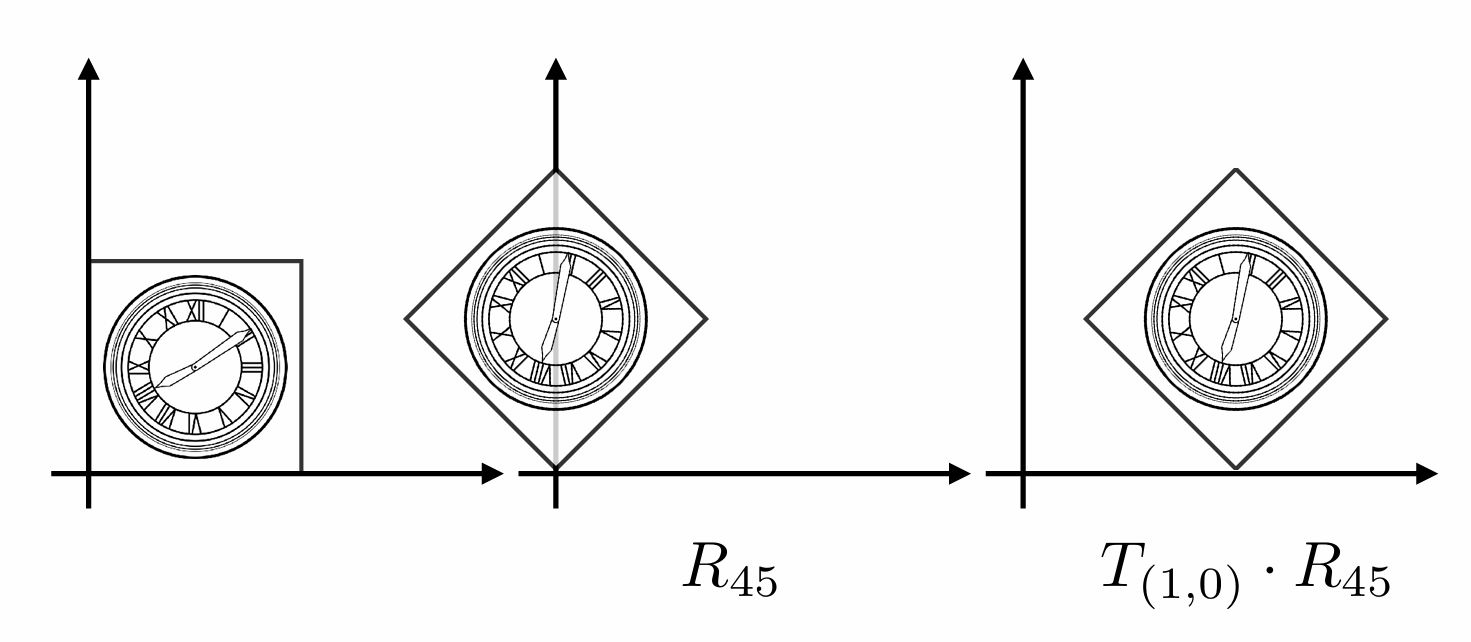
思考: 如何实现下图的变换?
- 方法一: 先平移, 再旋转 (可见, 先平移再旋转的效果与目标效果并不一致)
- 方法二: 先旋转, 再平移 (达到目标效果)
由此可见, 变换的顺序是很重要的 (矩阵的乘法是不满足交换律的)
变换矩阵的写法
向量将会从右向左逐个进行矩阵变换的应用 (在算式里是从左向右计算的)
\[A_n (A_{n-1} (A_{n-2} (\cdots (A_1 \cdot \vec{X})))) =\] \[A_n \cdot A_{n-1} \cdot A_{n-2} \cdots A_1 \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}\]但是, 矩阵虽然没有交换律, 但是有结合律, 因此我们可以先将多个变换矩阵相乘, 再将向量与结果相乘
\[A_n \cdot A_{n-1} \cdot A_{n-2} \cdots A_1 \cdot \vec{X} = \begin{bmatrix} A_n \cdot A_{n-1} \cdot A_{n-2} \cdots A_1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}\]变换的分解
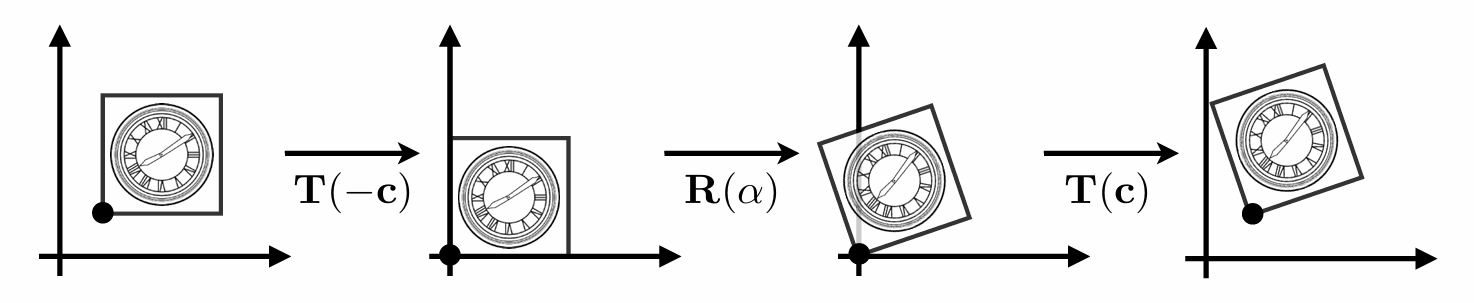
以任意点为中心的旋转
假设我们要以点 $c$ 为中心, 逆时针旋转 $\alpha$ 角度
那么我们可以将这个变换分解为以下三个变换的组合:
- 平移 $-c$ (整个图形一起平移到原点)
- 旋转 $\alpha$ (以原点为中心旋转)
- 平移 $c$ (整个图形平移到原来的位置)
矩阵的形式表示为(注意, 矩阵的乘法是从右向左的):
\[T_c \cdot R_{\alpha} \cdot T_{-c}\]