GAMES101 第4讲 变换(三维)
三维空间中的变换
三维空间的齐次坐标表示
- 3D的点: $(x, y, z, 1)^T$
- 3D的向量: $(x, y, z, 0)^T$
在三维齐次坐标中, 一个点的坐标 $(x/w, y/w, z/w)$ 可以表示为:
\[\begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} x/w \\ y/w \\ z/w \\ 1 \end{bmatrix} , w \neq 0\]三维空间的仿射变换的齐次坐标形式为:
\[\begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} a & b & c & t_x \\ d & e & f & t_y \\ g & h & i & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}\]其中, $ a, b, c, d, e, f, g, h, i $ 为线性变换矩阵的参数, $ t_x, t_y, t_z $ 为平移矩阵的参数
组合后的变换矩阵
组合后的变换矩阵的意义是: 先进行线性变换, 再进行平移变换
三维空间的仿射变换
缩放矩阵
缩放矩阵的对角线上的元素分别为 $s_x, s_y, s_z$, 最后一排为 $(0, 0, 0, 1)$
\[S_(s_x, s_y, s_z) = \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]平移矩阵
平移矩阵的最后一列分别为 $t_x, t_y, t_z$, 最后一排为 $(0, 0, 0, 1)$
\[T_(t_x, t_y, t_z) = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}\]旋转矩阵与欧拉角
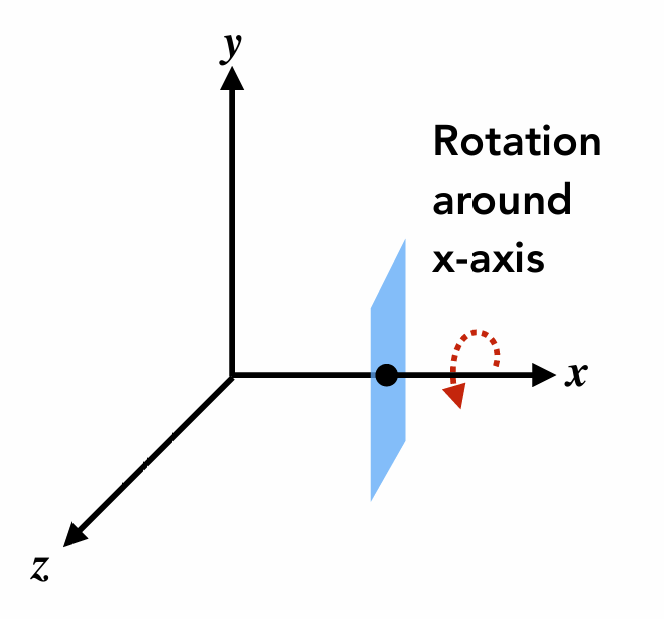 ss 绕着 $x-, y-, z-$ 轴旋转的矩阵分别如下:
ss 绕着 $x-, y-, z-$ 轴旋转的矩阵分别如下:
当绕着 $x-$ 轴旋转时, $x$ 不变, $y, z$ 会发生变化, 所以矩阵的第一行与第一列不变:
\[R_x(\theta) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos(\theta) & -\sin(\theta) & 0 \\ 0 & \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]当绕着 $z-$ 轴旋转时, $z$ 不变, $x, y$ 会发生变化, 所以矩阵的第三行与第三列不变:
\[R_z(\theta) = \begin{bmatrix} \cos(\theta) & -\sin(\theta) & 0 & 0 \\ \sin(\theta) & \cos(\theta) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]当绕着 $y-$ 轴旋转时, $y$ 不变, $x, z$ 会发生变化, 但是和绕着 $x-$ 轴和 $z-$ 轴旋转不同, 因为这里的 $y-$ 轴是右手坐标系, 也就是说 $ \vec{x} \times \vec{z} = \vec{-y} $, 而 $ \vec{z} \times \vec{x} = \vec{y} $, 所以矩阵的第二行与第二列不变, 但是第一行与第一列和第三行与第三列的变换与 $R_x(\theta)$ 和 $R_z(\theta)$ 是相反的:
\[R_y(\theta) = \begin{bmatrix} \cos(\theta) & 0 & \sin(\theta) & 0 \\ 0 & 1 & 0 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]将三个旋转矩阵组合起来, 可以得到任意旋转的矩阵:
\[R(\theta_x, \theta_y, \theta_z) = R_x(\theta_x) \cdot R_y(\theta_y) \cdot R_z(\theta_z)\]其中, $\theta_x, \theta_y, \theta_z$ 分别为绕着 $x-, y-, z-$ 轴旋转的角度, 称为欧拉角
在飞机的模拟中, 通常使用俯仰角(Pitch), 偏航角(Yaw), 滚转角(Roll) 来描述飞机的姿态
罗德里格斯公式(Rodrigues’ Formula)
绕着单位向量 $\vec{n}$ 旋转 $\alpha$ 角度的旋转, 该 $\vec{n}$ 过原点, 则旋转矩阵为:
\[R_(\mathbf{n}, \alpha) = \cos(\alpha) \mathbf{I} + (1 - \cos(\alpha)) \mathbf{n} \mathbf{n}^T + \sin(\alpha) \mathbf{N}\]向量 $\mathbf{n}$ 的叉乘矩阵 $\mathbf{N}$ 定义如下:
\[\mathbf{N} = \begin{bmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{bmatrix}\]如果要绕着任意轴旋转, 可以先将所有东西移动到使得旋转轴过原点, 然后再进行旋转, 最后再移动回去