GAMES101 第4讲 观察变换(视图变换与投影变换)
观察变换
观察变换(Viewing Transform)是将世界坐标系中的物体变换到裁剪坐标系中的过程
视图/相机变换
相机坐标系
视图/相机变换(View/Camera Transform)是将世界坐标系中的物体变换到相机坐标系中的过程
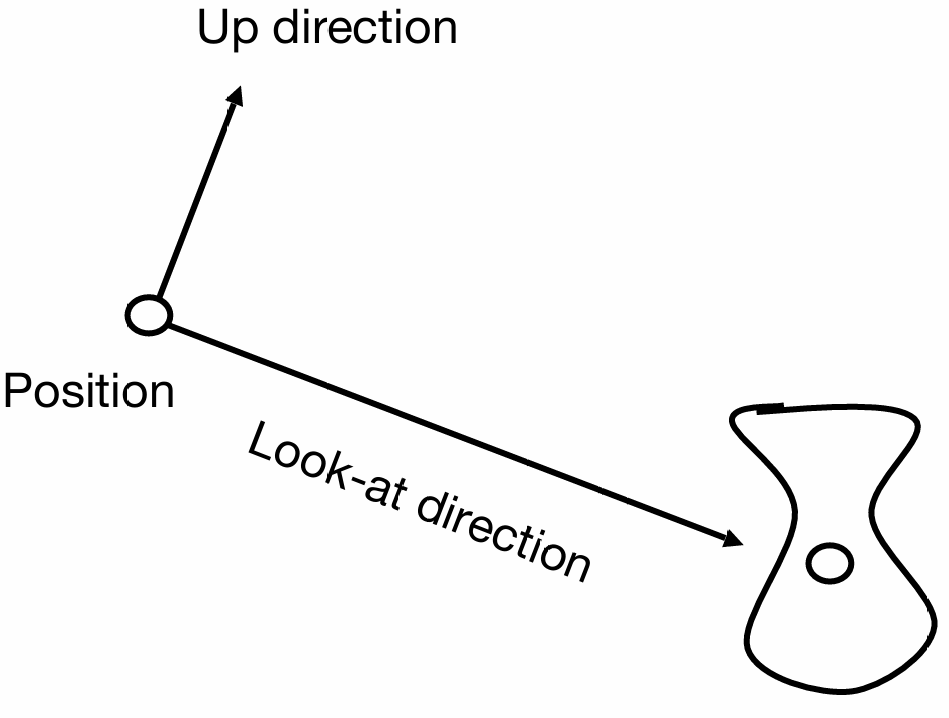
视图变换是在摆放照相机, 所以我们要定义相机的参数:
- 坐标(Position): $\vec{e}$
- 观察方向(Look At/Gaze): $\hat{g}$
- 上方向(Up): $\hat{t}$
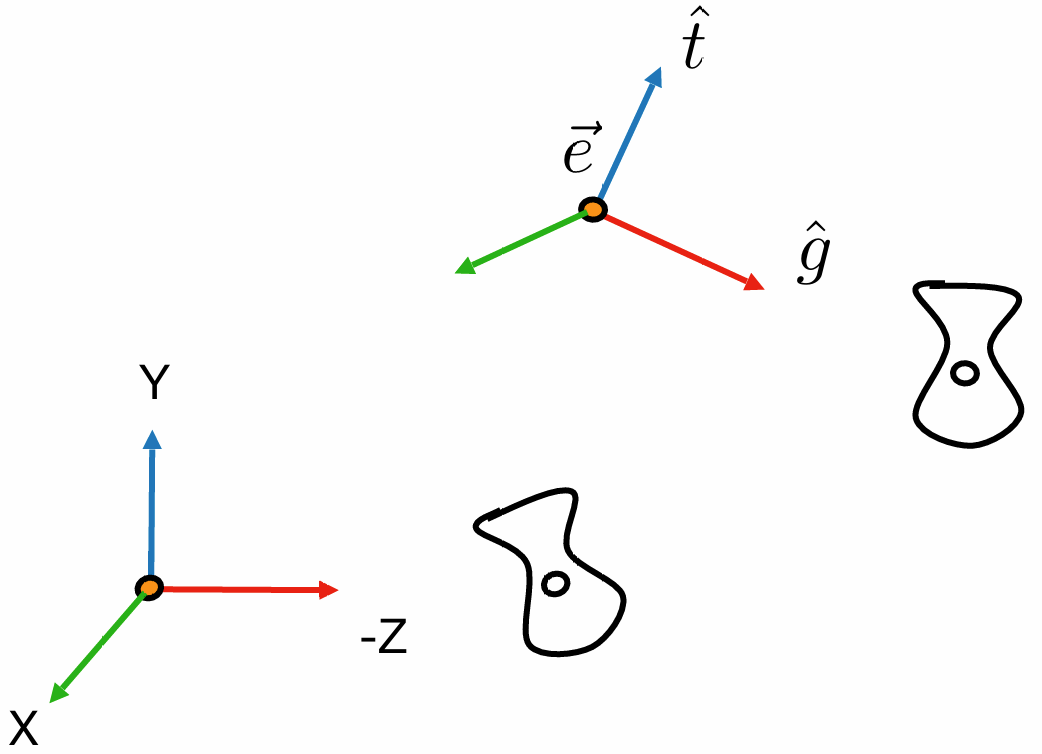
为了方便计算和理解, 我们认为相机坐标系是:
- 相机坐标永远位于原点
- 相机的上方向永远是 $y$ 轴正方向
- 相机的观察方向永远是 $z$ 轴负方向, 即 $-z$方向
- 所有物体随着相机的移动而移动
视图变换矩阵
假如相机本身的坐标是 $\vec{e}$, 观察方向是 $\hat{g}$, 上方向是 $\hat{t}$, 那么将其转换为相机坐标系的操作则有:
- 将 $\vec{e}$ 移动到原点
- 将 $\hat{g}$ 转换为 $-z$ 轴
- 将 $\hat{t}$ 转换为 $y$ 轴
- 将 $\hat{g} \times \hat{t}$ 转换为 $x$ 轴
将以上操作写成矩阵的形式:
\[M_{view} = R_{view} \cdot T_{view}\]其中 $R_{view}$ 为旋转矩阵部分, $T_{view}$ 为平移矩阵部分
\[T_{view} = \begin{bmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix}\]通过从$\hat{g} \times \hat{t}, \hat{t}, -\hat{g}$ 旋转到 $x, y, z$ 轴来直接推导旋转矩阵较为困难
但是已知 $x, y, z$ 轴的单位向量 , 求旋转到 $\hat{g} \times \hat{t}, \hat{t}, -\hat{g}$ 的旋转矩阵 $R_{view}^{-1}$ 是比较容易的
同时又因为旋转矩阵是正交矩阵, 所以有 $R_{view}^T = R_{view}^{-1}$
\[R_{view}^{-1} = \begin{bmatrix} x_{\hat{g} \times \hat{t}} & x_{\hat{t}} & x_{-\hat{g}} & 0 \\ y_{\hat{g} \times \hat{t}} & y_{\hat{t}} & y_{-\hat{g}} & 0 \\ z_{\hat{g} \times \hat{t}} & z_{\hat{t}} & z_{-\hat{g}} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\] \[R_{view} = (R_{view}^{-1})^T = \begin{bmatrix} x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\ x_{\hat{t}} & y_{\hat{t}} & z_{\hat{t}} & 0 \\ x_{-\hat{g}} & y_{-\hat{g}} & z_{-\hat{g}} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]投影变换
投影变换(Projection Transform)是将相机坐标系中的物体变换到裁剪坐标系中的过程
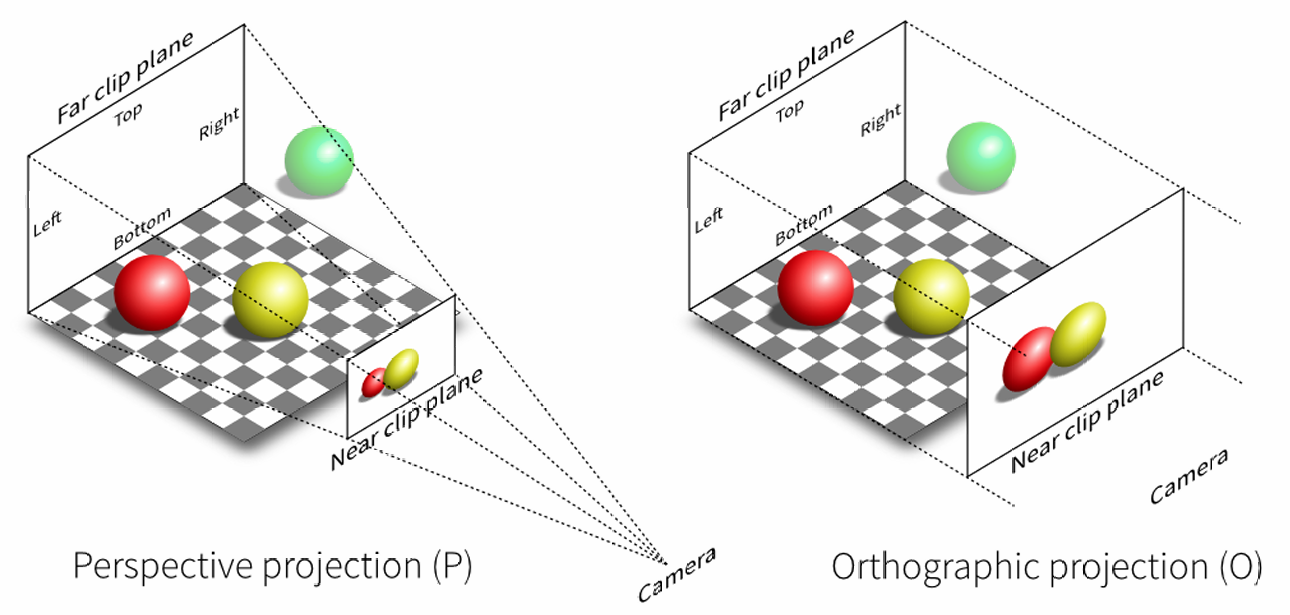
投影变换分为正交投影(Orthographic Projection) 和 透视投影(Perspective Projection)
正交投影
较为简单的理解:
- 相机放在原点, 观察方向是 $-z$ 轴, 向上方向是 $y$ 轴
- 将物体的 $z$ 坐标直接扔掉, 保留 $x, y$ 坐标
- 将 $x, y$ 坐标映射到 $[-1, 1]^2$ 的范围内(方便后续裁剪)
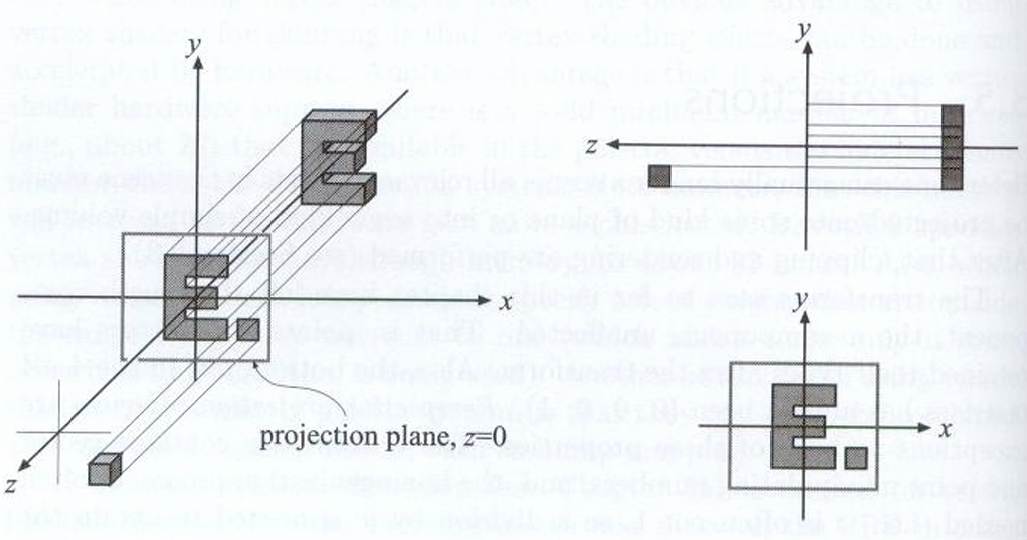
在图形学中的正交投影:
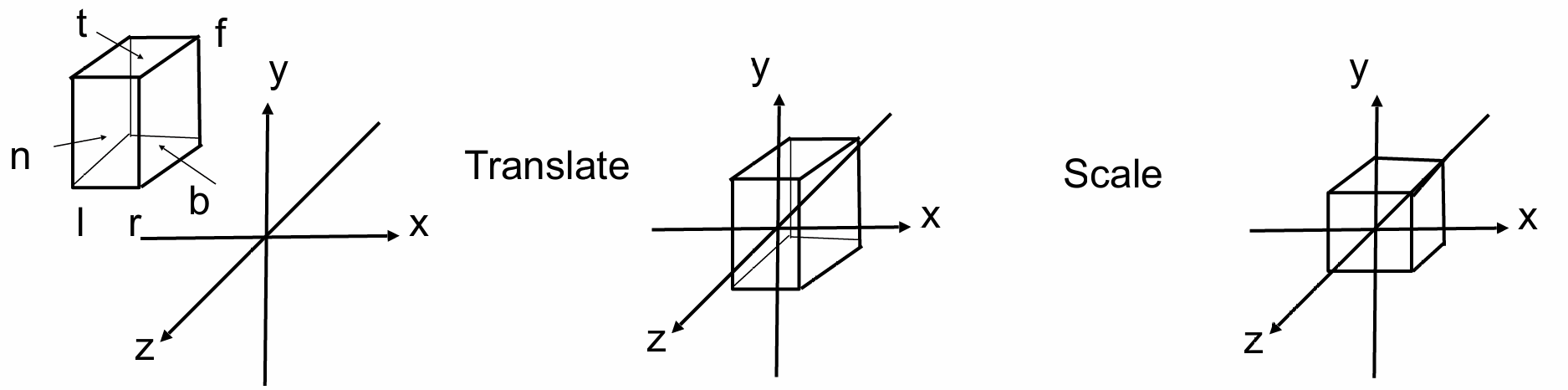
- 在空间中定义一个立方体, 并规定其左右, 下上, 远近的边界分别在 $x, y, z$ 轴上的范围 $[l, r], [b, t], [f, n]$
- 将这个立方体映射到 $[-1, 1]^3$ 的正则立方体(Canonical Cube)中
- 将立方体的中心移动到原点
- 将 $x, y, z$ 轴分别拉伸到 $[-1, 1]$ 的范围内
- 注意: 不会抛弃 $z$ 轴的值, $z$ 值越小, 距离相机越远
矩阵的形式为(先平移再缩放):
\[M_{ortho} = S_{ortho} \cdot T_{ortho} = \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & 0 \\ 0 & \frac{2}{t - b} & 0 & 0 \\ 0 & 0 & \frac{2}{n - f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r + l}{2} \\ 0 & 1 & 0 & -\frac{t + b}{2} \\ 0 & 0 & 1 & -\frac{n + f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix}\]左右手坐标系的不同会导致 $z$ 轴的方向不同, 所以在计算时要注意
透视投影
透视投影使用的最广泛的投影方式, 也是人眼看到的世界的投影方式
回顾: $(x, y, z, 1)$ 与 $(kx, ky, kz, k)$ 表示的是三维空间的同一个点 $(x, y, z)$ , 注意$k \neq 0$
因此, $(xz, yz, z^2, z)$ 与 $(x, y, z, 1)$ 表示的是三维空间的同一个点 $(x, y, z)$ , 注意$z \neq 0$
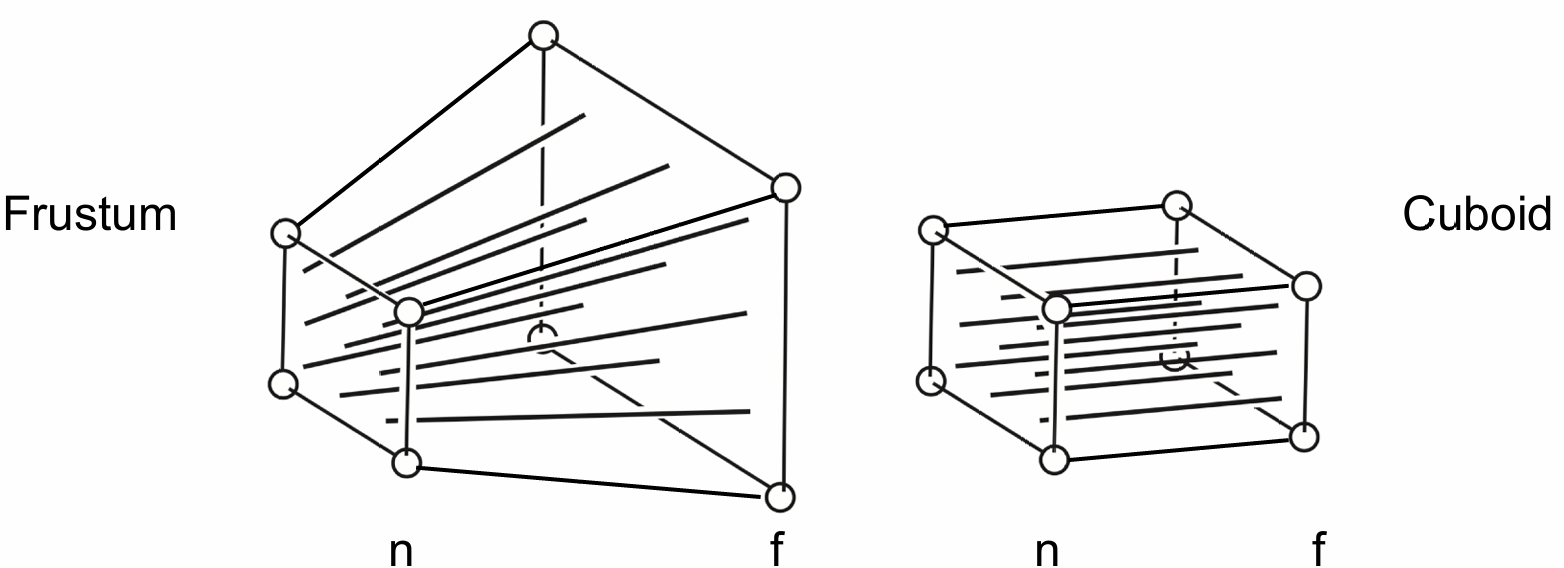
- 先将视锥体的远端平面”挤压“到和近端平面齐平的位置, 此时成为了一个立方体
- 将立方体映射到 $[-1, 1]^3$ 的正则立方体(Canonical Cube)中, 操作类似于正交投影
挤压的过程中为了便于理解和计算, 我们规定:
近端平面的所有坐标都不变, 视锥体远端平面的 $z$ 坐标也都不变, 远端平面中心点的所有坐标也不发生变化, 此时挤压操作只有唯一解
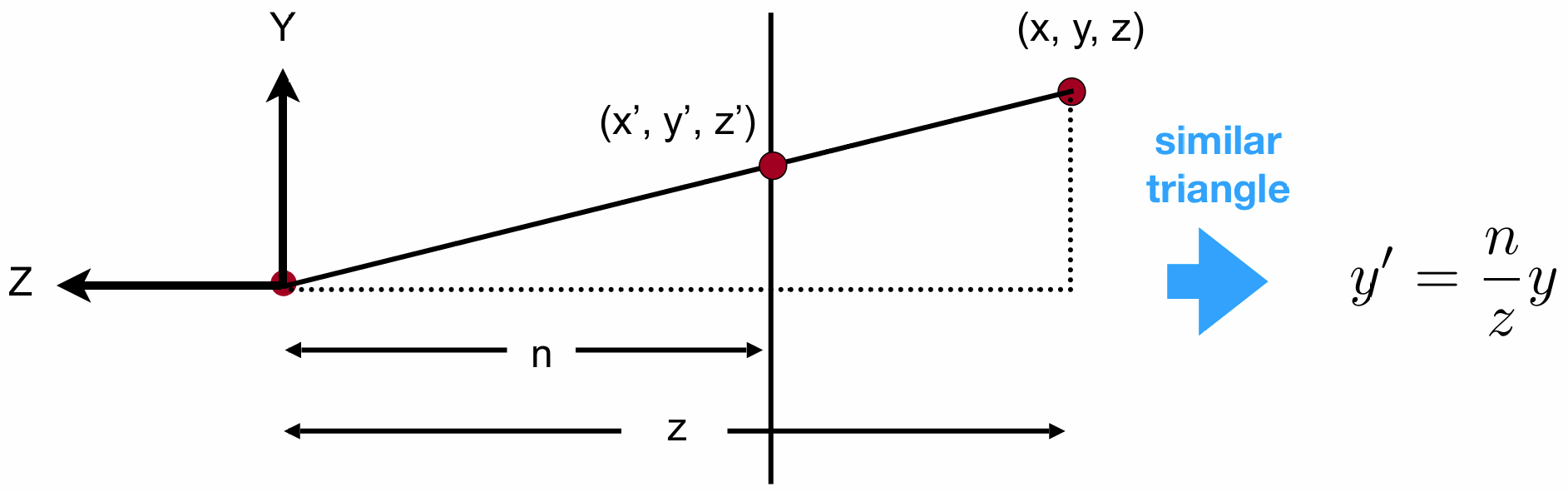
根据相似三角形, 所有点的
\[x' = \frac{n}{z}x\] \[y' = \frac{n}{z}y\]在齐次坐标中, 有:
\[\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} \rightarrow \begin{bmatrix} \frac{nx}{z} \\ \frac{ny}{z} \\ unknown \\ 1 \end{bmatrix} == \begin{bmatrix} nx \\ ny \\ still unknown \\ z \end{bmatrix}\]我们想要知道挤压矩阵 $M_{persp \rightarrow ortho}^ {4 \times 4}$ 的形式, 使得:
\[M_{persp \rightarrow ortho}^ {4 \times 4} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} nx \\ ny \\ unknown \\ z \end{bmatrix}\]可以反推出:
\[M_{persp \rightarrow ortho}^ {4 \times 4} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & -1 & 0 \end{bmatrix}\]又由于近端平面的所有坐标都不变, 我们假设有一个近平面上的点 $(x, y, n)$, 则有:
\[M_{persp \rightarrow ortho}^ {4 \times 4} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} nx \\ ny \\ unknown \\ z \end{bmatrix} \xrightarrow{z = n} \begin{bmatrix} x \\ y \\ n \\ 1 \end{bmatrix} \rightarrow \begin{bmatrix} x \\ y \\ n \\ 1 \end{bmatrix} == \begin{bmatrix} nx \\ ny \\ n^2 \\ n \end{bmatrix}\]我们可以推断出矩阵的第三行 $\begin{bmatrix}0 & 0 & A & B \end{bmatrix}$ 满足:
\[\begin{bmatrix} 0 & 0 & A & B \end{bmatrix} \begin{bmatrix} x \\ y \\ n \\ 1 \end{bmatrix} = n^2\]由于远端平面的中心点的坐标不变, 我们假设有一个远平面上的中心点 $(0, 0, f)$, 则有:
\[M_{persp \rightarrow ortho}^ {4 \times 4} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} nx \\ ny \\ unknown \\ z \end{bmatrix} \xrightarrow{x = 0 y = 0 z = f} \begin{bmatrix} 0 \\ 0 \\ f \\ 1 \end{bmatrix} \rightarrow \begin{bmatrix} 0 \\ 0 \\ f \\ 1 \end{bmatrix} == \begin{bmatrix} 0 \\ 0 \\ f^2 \\ f \end{bmatrix}\]我们可以推断出矩阵的第三行 $\begin{bmatrix}0 & 0 & A & B \end{bmatrix}$ 满足:
\[\begin{bmatrix} 0 & 0 & A & B \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ f \\ 1 \end{bmatrix} = f^2\]综上有:
\[An + B = n^2 \\ Af + B = f^2\]解方程得到:
\[A = n + f \\ B = -nf\]所以挤压操作的矩阵形式为:
\[M_{persp \rightarrow ortho}^ {4 \times 4} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & -nf \\ 0 & 0 & -1 & 0 \end{bmatrix}\]透视投影的矩阵形式为(先挤压再正交):
\[M_{persp} = M_{ortho} \cdot M_{persp \rightarrow ortho} = M_{ortho} \cdot M_{persp \rightarrow ortho}^ {4 \times 4}\]思考: 在挤压操作时, 远端平面与近端平面中间的 $z$ 坐标是如何变化的? 变得更远(z更小)还是更近(z更大)?