GAMES101 第5讲 光栅化(三角形)

在观测变换之后, 场景内所有物体都会被变换到$(-1, 1)^3$的规范立方体内, 那么下一步就是光栅化

透视投影

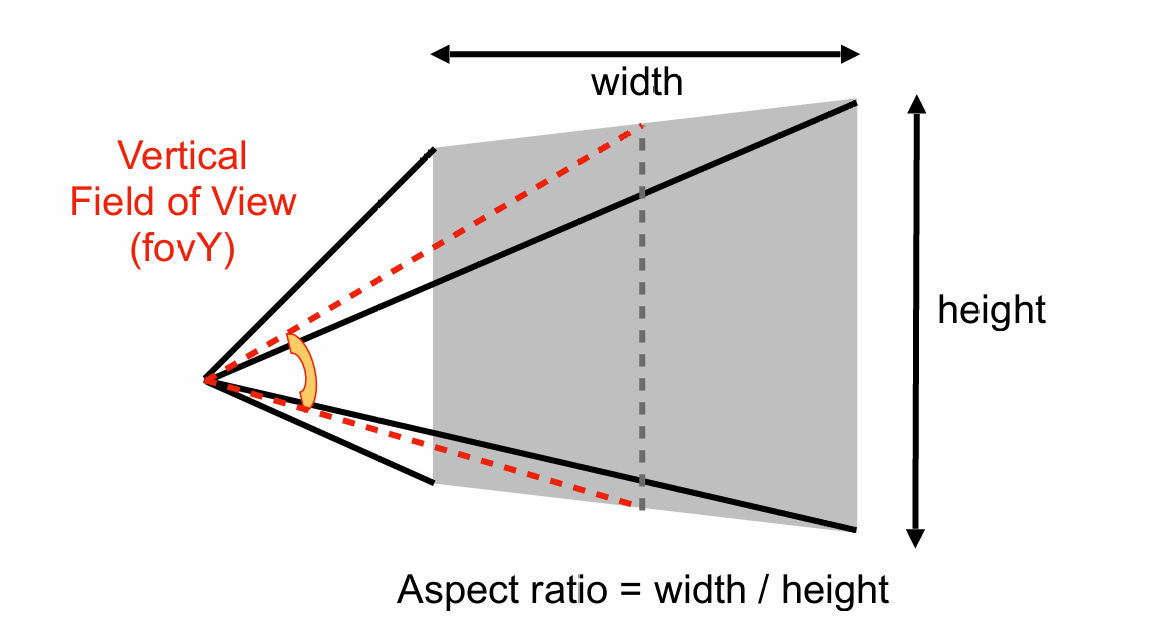
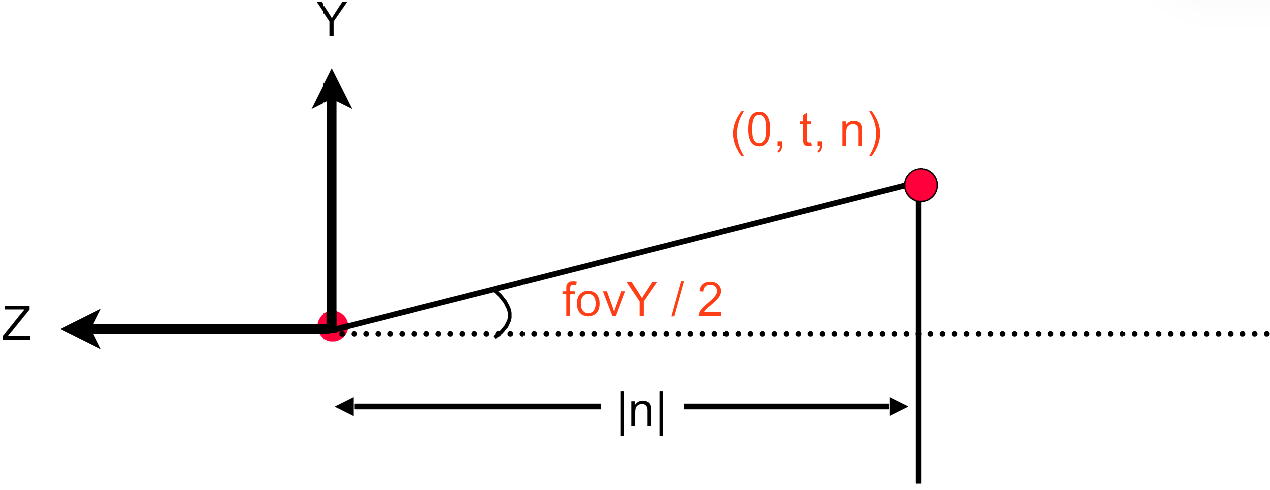
在正交投影中, 远平面近平面是由 $z$ 坐标决定的, 左平面右平面是由 $x$ 坐标决定的, 上平面下平面是由 $y$ 坐标决定的, 而在透视投影中, 远近平面同样是由 $z$ 坐标决定的, 而左右平面和上下平面则用fovY(field of view in Y为视野角)和aspect ratio(宽高比)来决定

• 竖直方向的视野角 fovY: 两条红线所夹的角度
• 宽高比 aspect ratio: $\frac{width}{height}$

\[tan(\frac{fovY}{2}) = \frac{top}{|near|}\] \[aspect = \frac{right}{top}\] \[bottom = -top, left = -right\]

将规范立方体的内容绘制到屏幕

相关定义

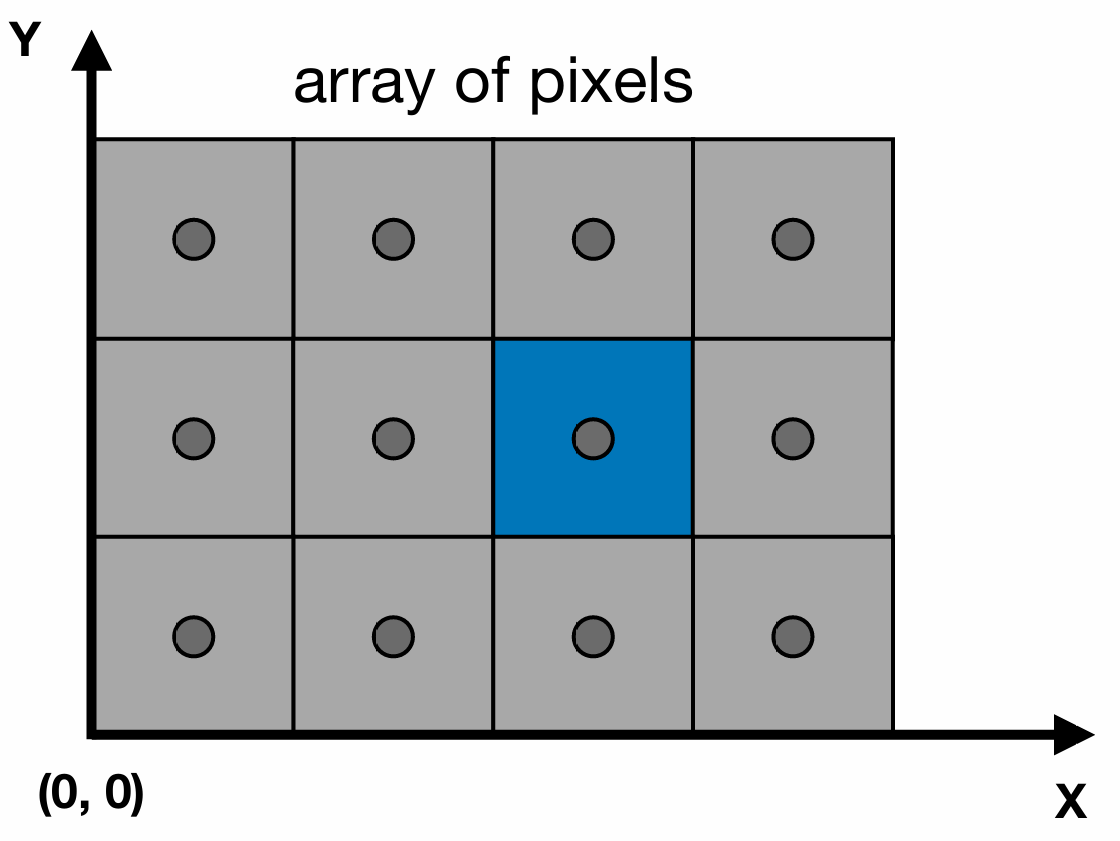
屏幕

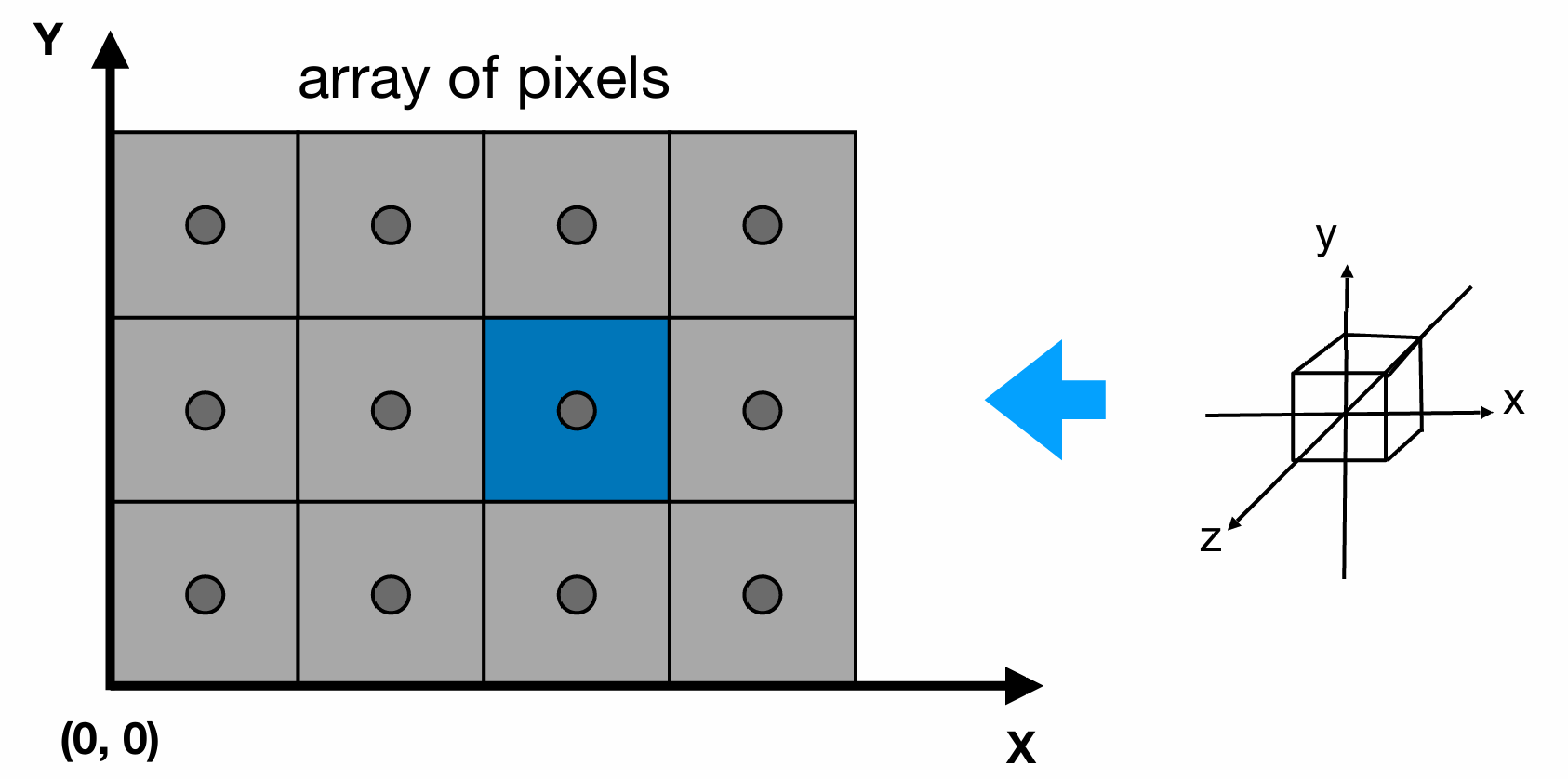
在图形学上, 屏幕是:

• 一个二维的像素数组
• 阵列大小: 分辨率(Resolution), 例如1920x1080

光栅

• 光栅: 德语Raster, 意为”屏幕”
• 光栅化: 绘制到屏幕上的过程

像素

• Pixel: Picture Element, 图片的基本单元
• 像素是一个小的矩形区域, 只有单一颜色
• 颜色由RGB(红绿蓝)三个分量组成

屏幕空间

• 屏幕空间(Screen Space): 屏幕上的坐标系
• 假设左下角是$(0, 0)$, 右上角是$(width, height)$
• 像素的坐标是 $(x, y)$ 形式的, 每个坐标都是整数, 以像素方块的左下角为准
• 像素的范围是 $[0, width-1]$ 到 $[0, height-1]$
• 像素 $(x, y)$ 的中心是 $(x+0.5, y+0.5)$

视口变换

• 与 $z$ 坐标无关
• 将 $[-1, 1]^2$ 映射到 $[0, width] \times [0, height]$

第一步: 直接拉伸到屏幕空间

\[M_{viewport} = \begin{bmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} \\ 0 & \frac{height}{2} & 0 & \frac{height}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

可以看到, 是执行了两个操作:

• 先将其缩放到屏幕大小的一半
• 再将其平移至屏幕中心

光栅化

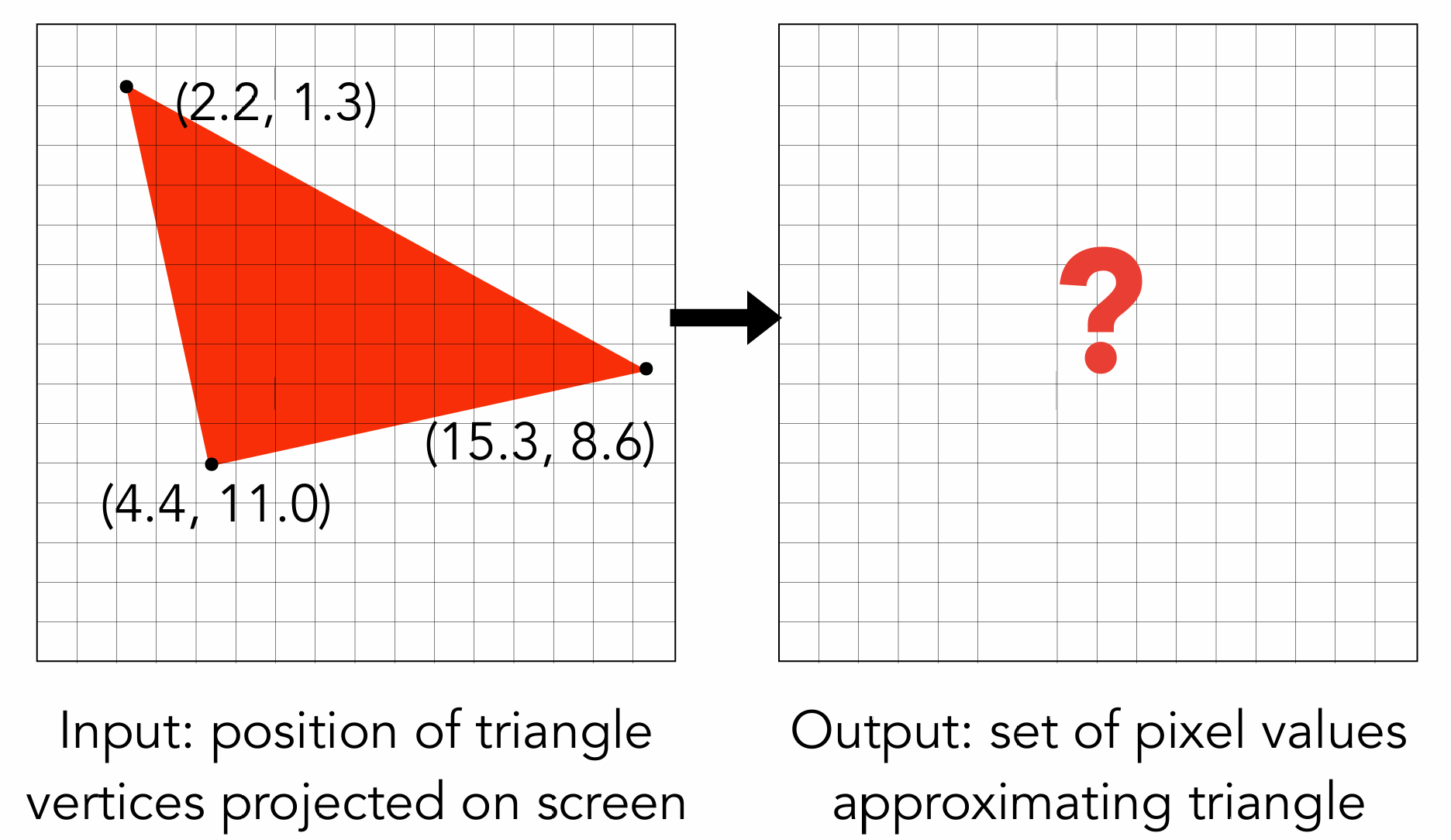
三角形到像素的光栅化

为什么是三角形?:

1. 三角形是最基础的多边形
2. 任何多边形都可以被分解为三角形
3. 三角形内部的点都一定在三角形的平面内
4. 三角形的内外判断是最简单的
5. 三角形很适合进行插值(重心坐标插值)

我们需要考虑, 像素的中心点与三角形的边界的关系

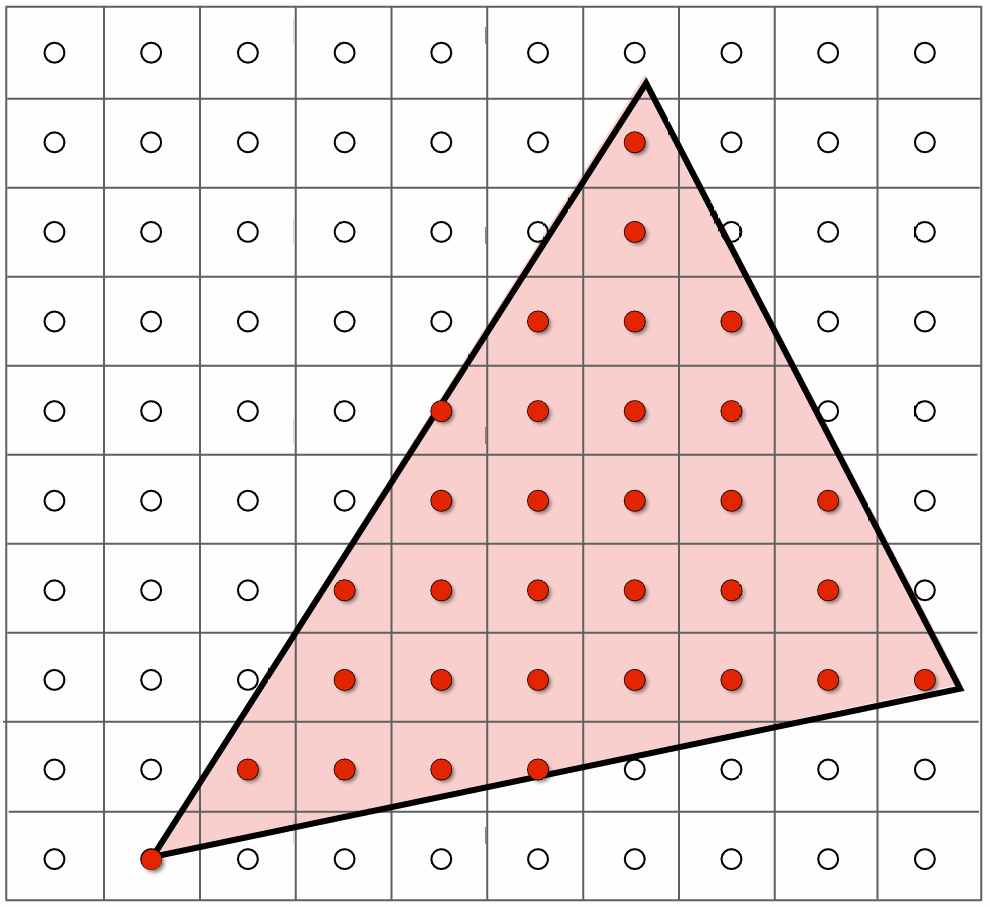
采样的概念

采样: 给定一个连续的函数, 在不同的位置上取样, 得到离散的值 (即, 采样是一个函数的离散化的过程)

光栅化中的采样则是利用像素中心, 对屏幕空间进行采样

2D采样——光栅化

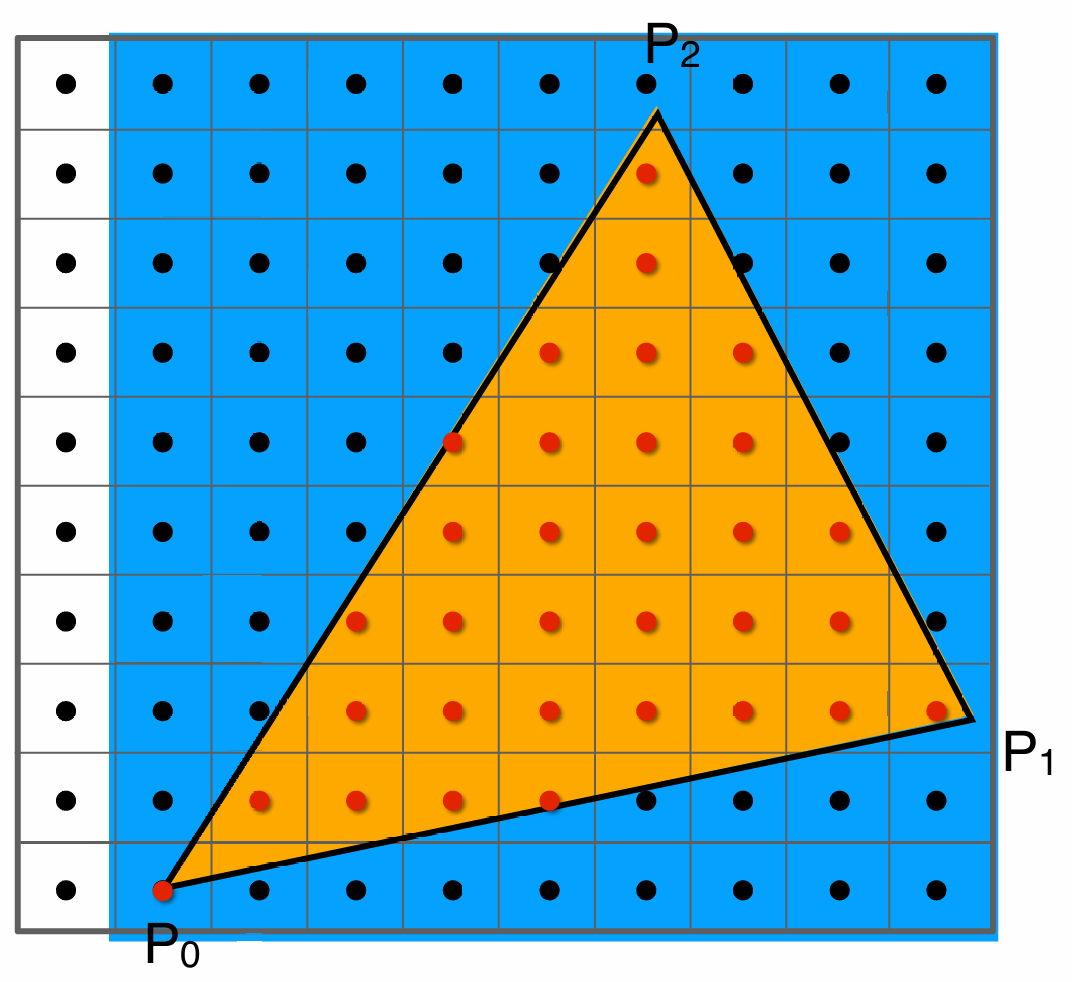
给定一个三角形, 判断像素的中心是否在三角形内部

以函数的形式表示:

\[inside(tri, x, y) = \begin{cases} 1, & \text{if } (x, y) \text{ is inside } tri \\ 0, & \text{otherwise} \end{cases}\]

以cpp代码的形式表示:

for(int x = 0; x < x_max; ++x) {
    for(int y = 0; y < y_max; ++y) {
        image[x][y] = inside(tri, x + 0.5, y + 0.5);
    }
}

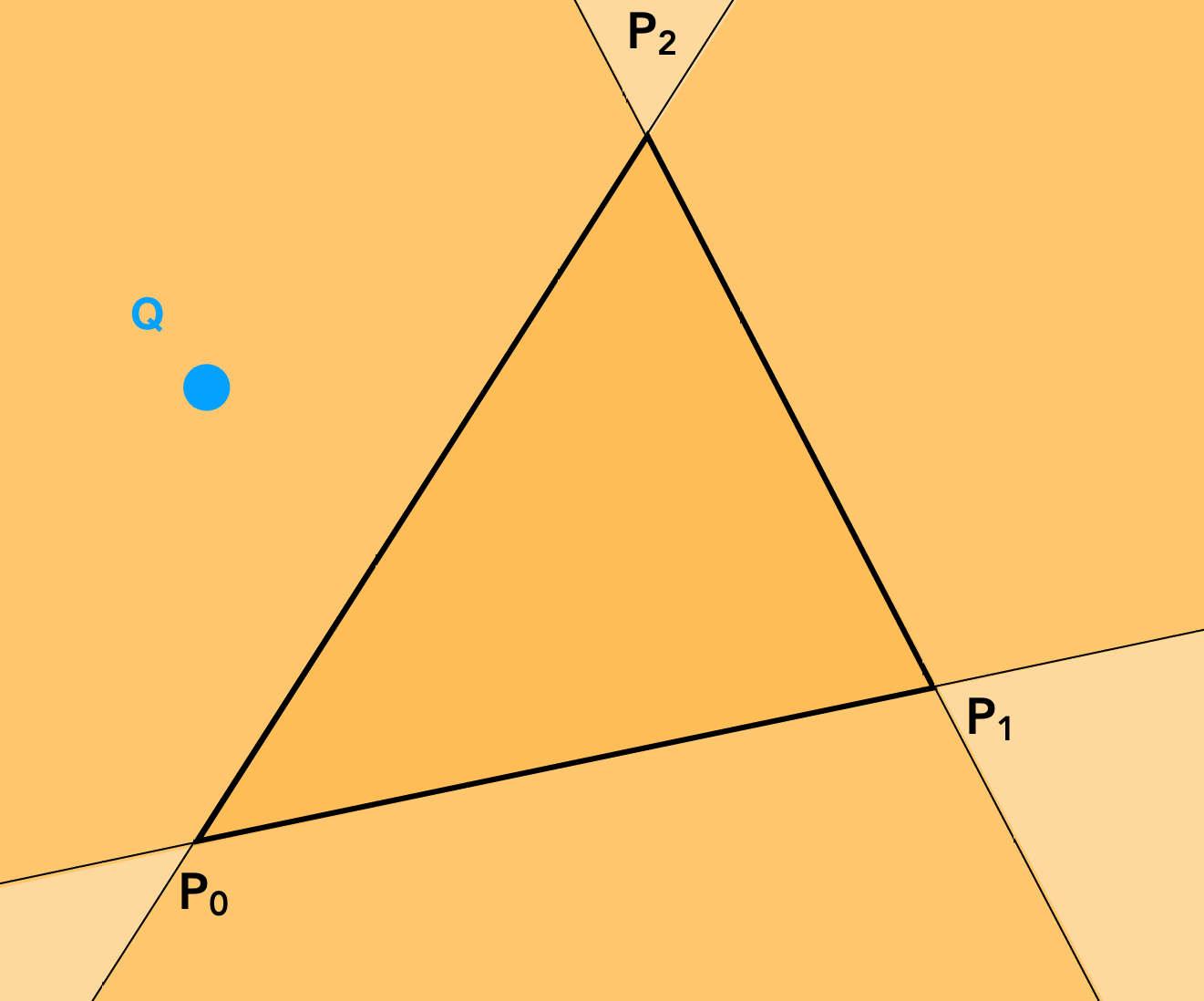
如何判断点是否在三角形内部?

• 三角形的三个顶点分别为 $P_0, P_1, P_2$
• 点 $Q$ 在三角形所在的平面上

用叉乘来判断点是否在三角形内部:

\[P_0P_1 \times P_0Q \geq 0: Q 在 P_0P_1 的左侧\] \[P_1P_2 \times P_1Q \geq 0: Q 在 P_1P_2 的左侧\] \[P_2P_0 \times P_2Q \leq 0: Q 在 P_2P_0 的右侧\]

综上, 当在同一侧时, 叉乘的结果应该同号, 所以 $Q$ 在三角形外部

如果点在三角形的边上, 则叉乘的结果为0, 则我们自己定义其在三角形内部还是外部, 在一些图形API中, 会进行较为严格的定义(如OpenGL中, 左边和上边是在三角形内部, 右边和下边是在三角形外部)

优化

如果左边一竖列的像素都在三角形外部, 那么这一竖列的像素都不需要计算, 可以直接跳过

对于图上蓝色的区域, 我们叫做三角形的包围盒

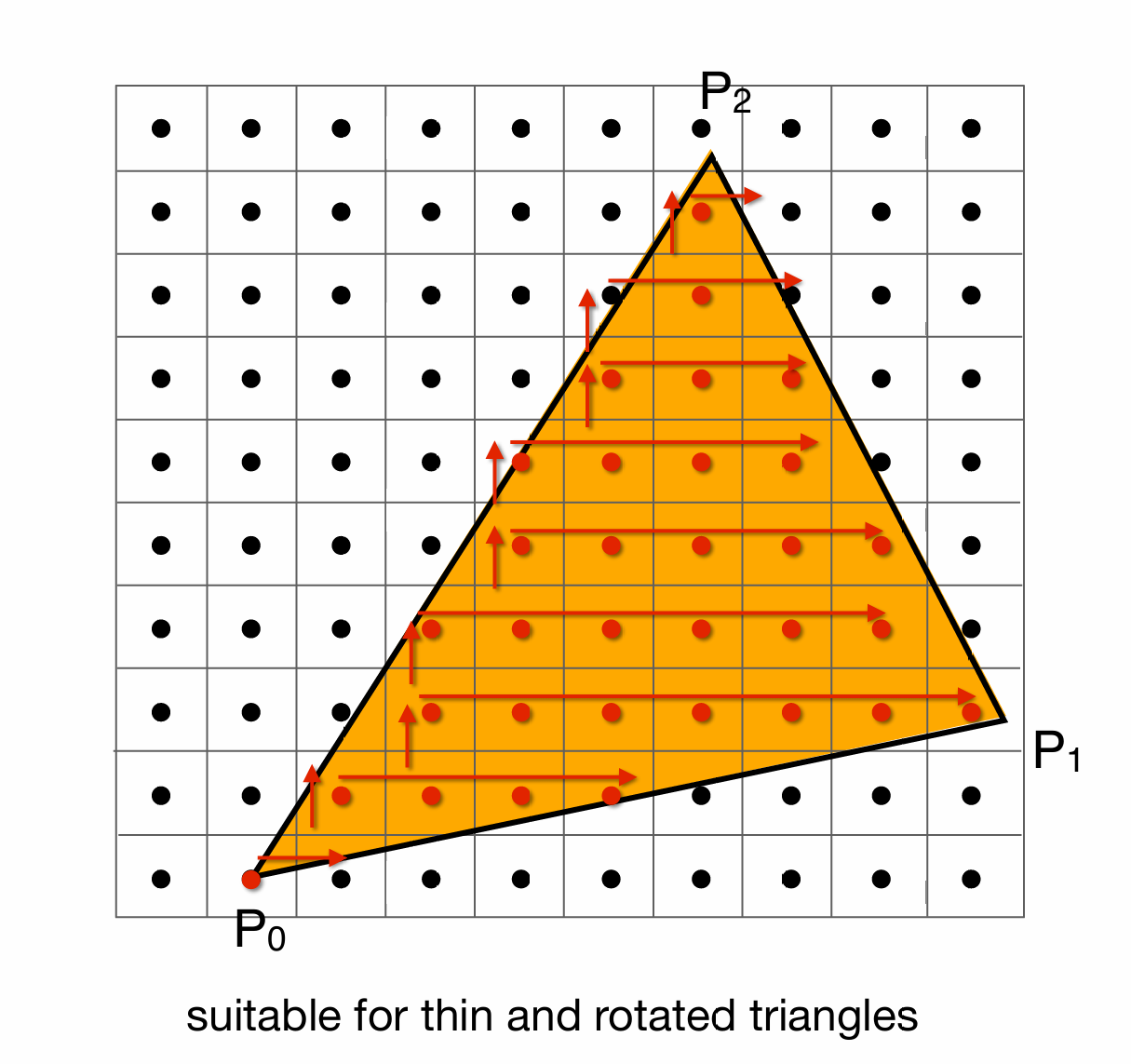
针对较为窄长或旋转过的三角形, 它的包围盒所占像素相较于三角形覆盖的像素的像素来说, 相差较大, 所以我们可以将这种三角形的包围盒进行优化

对于上图中的三角形, 我们可以对其每一行像素都计算其最左最右, 从而减少像素的计算量