GAMES101 第6讲 光栅化(抗锯齿)
抗锯齿
什么是抗锯齿
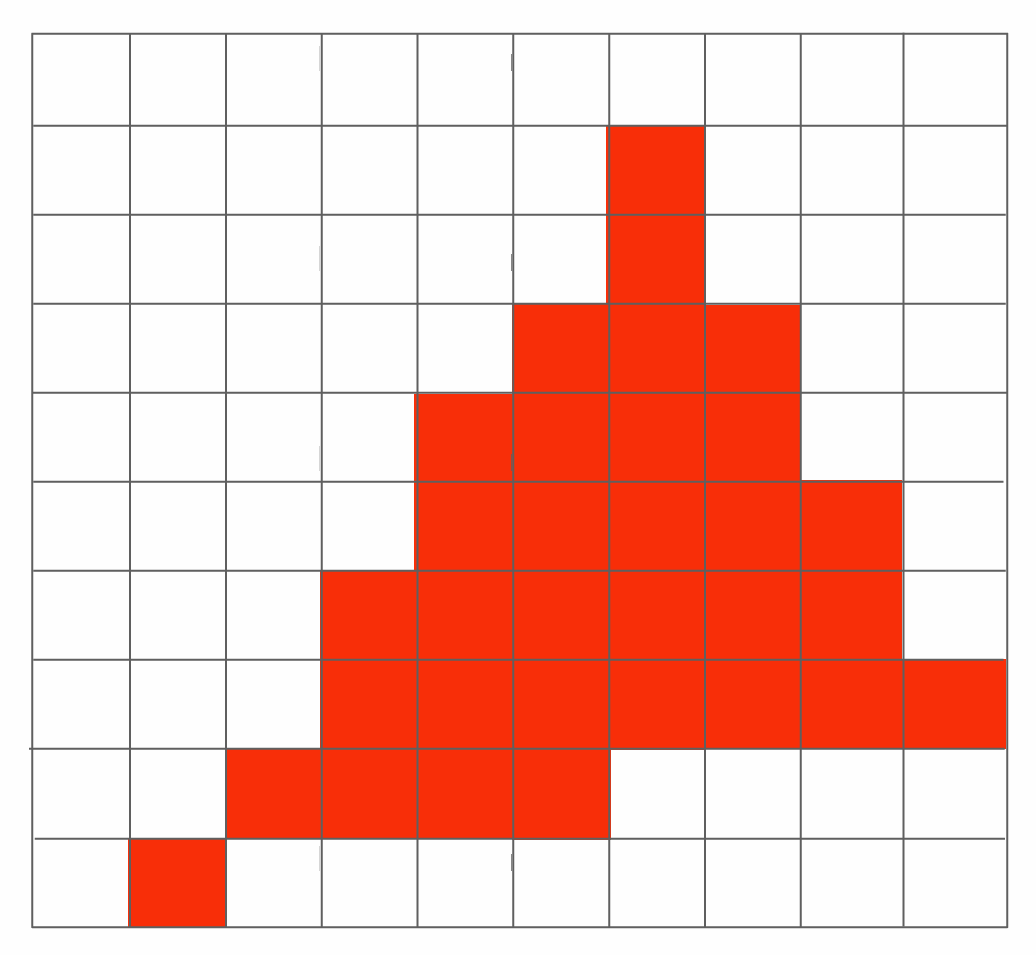
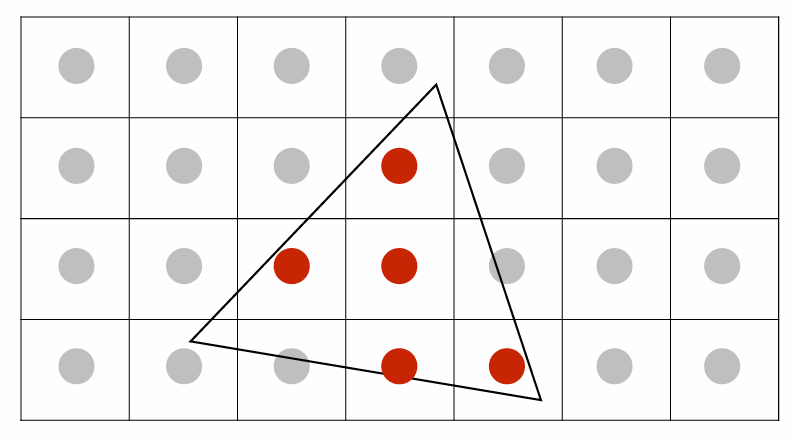
对每个像素的中心坐标进行采样以判断该像素是否在三角形内部
以上图形显示结果与实际三角形形状并不一致, 因为我们只对像素中心进行采样, 但实际上像素是一个矩形, 有可能只有一个角落在三角形内部, 但整个像素却被认为在三角形外部
实际上我们期望看到的三角形应该如下图所示
为了避免出现锯齿的现象(如下图), 我们要做的内容便是抗锯齿(反走样 Anti-aliasing)
采样理论
因为采样精度有限而造成的错误: 走样(Aliasing)
- 锯齿(Jaggies): 在空间上采样精度不足
- 摩尔纹(Moire): 采样率不匹配
- 车轮效应(Wagon Wheel Effect): 在时间上采样精度不足
- ……
走样的原因:
- 信号改变的速度太快但采样速度不够
抗锯齿的实践
抗锯齿(反走样)方法: 在采样之前做模糊处理
未进行模糊处理直接采样:
先进行模糊处理再采样:
实际运用的效果(左图为未进行抗锯齿处理, 右图为进行抗锯齿处理):
时域和频域
傅里叶变换
傅里叶变换可以将一个图形从时域(Time Domain)转换到频域(Frequency Domain), 从而可以更好的理解图形的特性
傅里叶变换: 通过傅里叶级数展开,一个周期函数 (f(x)) 可以表示为以下形式: [ f(x) = \frac{A}{2} + \frac{2A \cos(t\omega)}{\pi} - \frac{2A \cos(3t\omega)}{3\pi} + \frac{2A \cos(5t\omega)}{5\pi} - \frac{2A \cos(7t\omega)}{7\pi} + \dots ]
- (A/2): 表示直流分量(函数的平均值)。
- 余弦项和正弦项: 表示函数的频率分量,频率越高,描述越精细。
高频需要高采样率
对于一个函数来说, 函数本身有一定的频率, 我们的采样也有相应的频率, 如果采样频率不够高, 那么就会出现无法跟随函数频率变化的现象, 从而导致走样
通过频率来分析走样
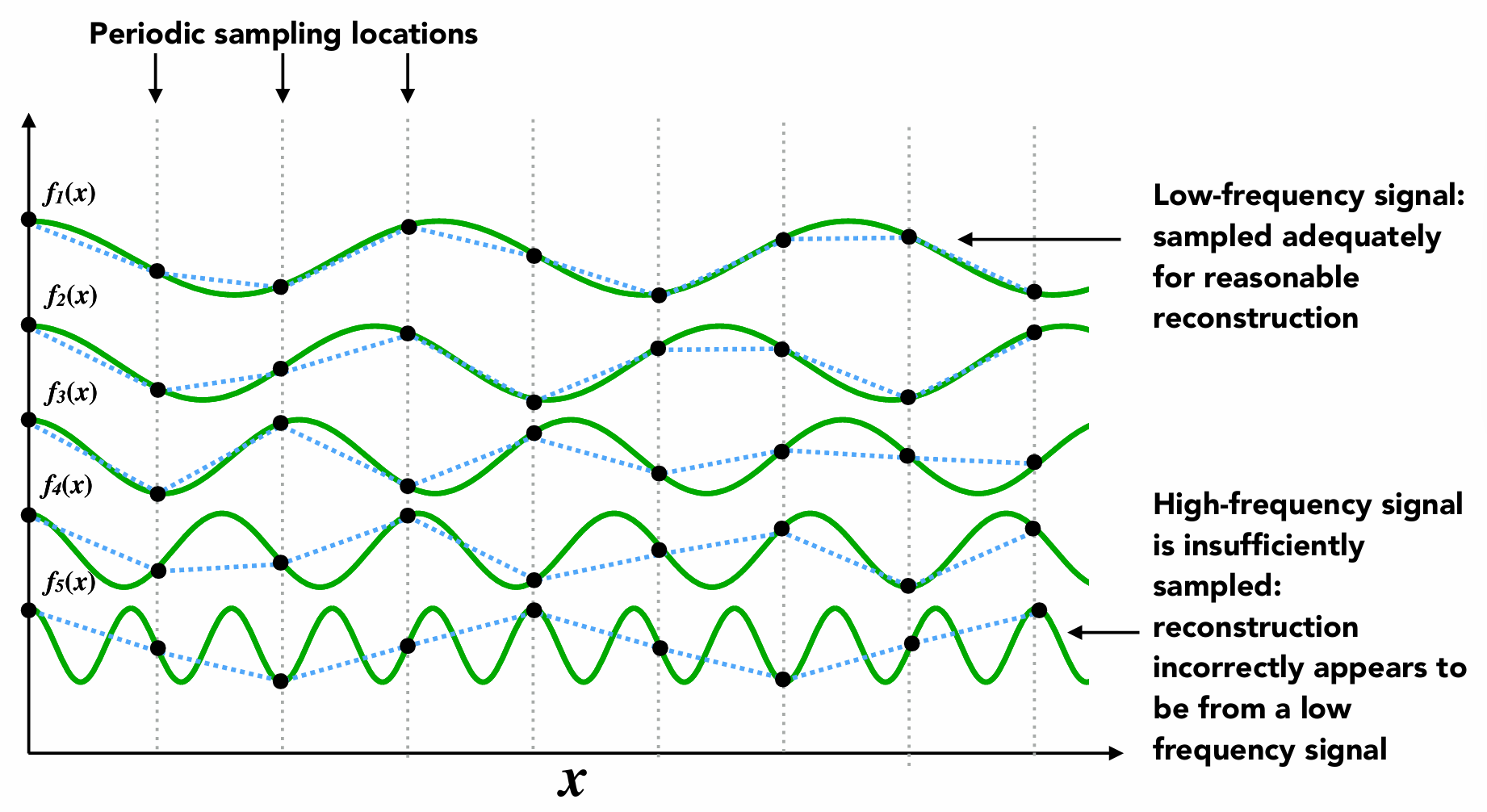
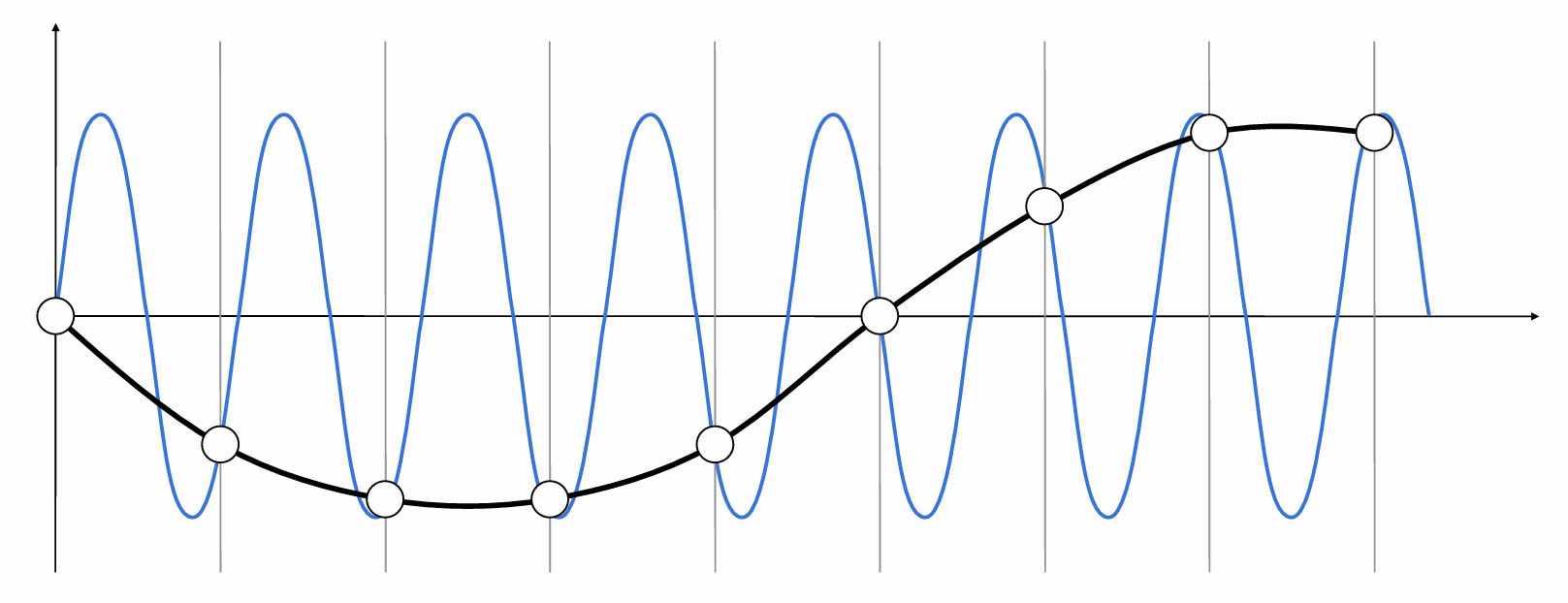
在下图情况中, 我们使用同一种采样方法(采样频率相同), 对于两种不同频率的信号, 出现了相同的采样结果, 从而导致了走样
频谱分析
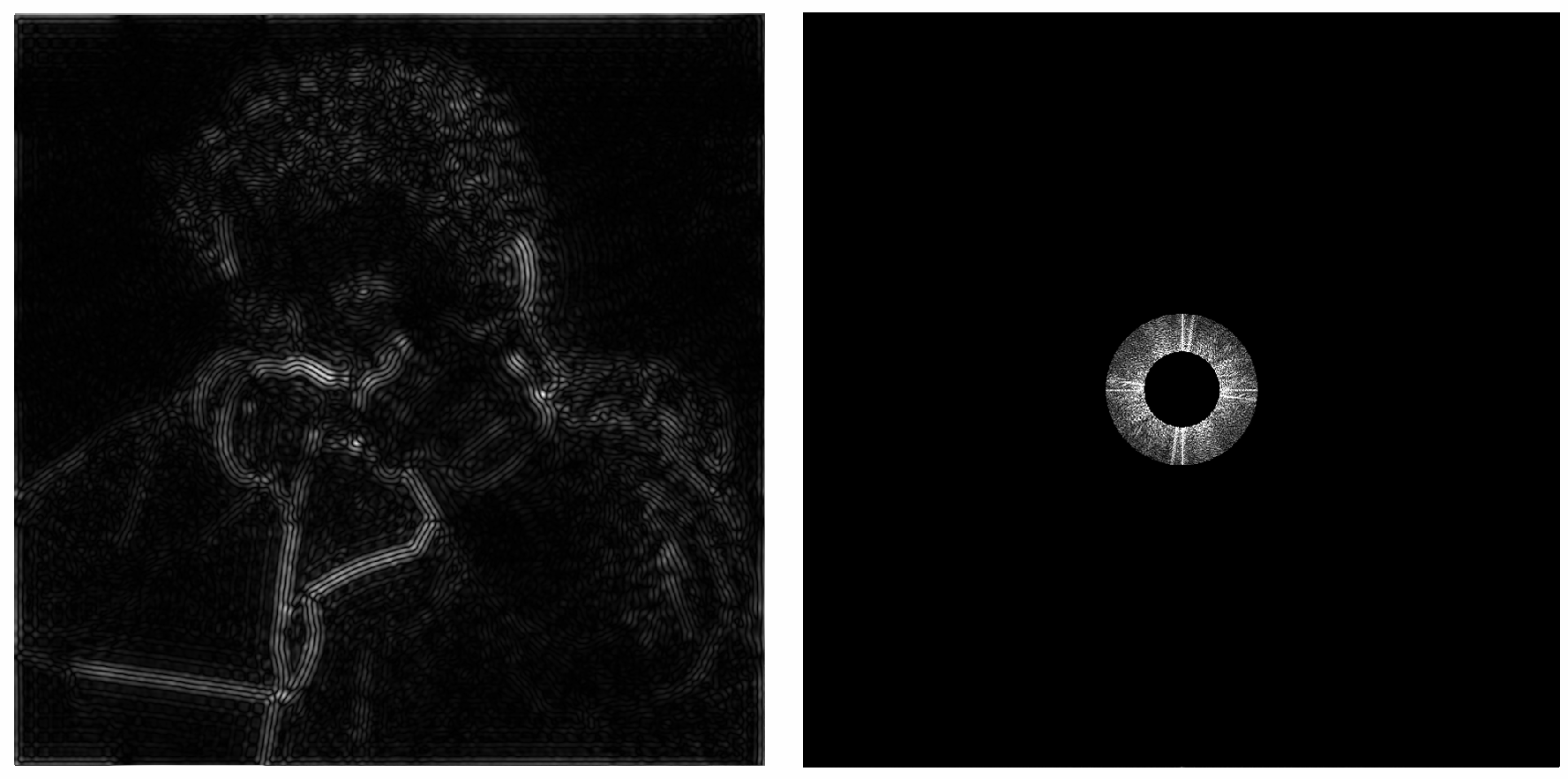
这张图片展示了图像在时域和频域的表现:
- 左侧:这是图像在时域中的表示,即原始图像的空间分布(像素值随位置的变化)。
- 每个像素点的灰度值表示亮度。
- 这种表示直观地展示了图像的内容和细节,例如轮廓、边缘和纹理。
- 右侧:这是图像在频域中的表示,通常是通过傅里叶变换(Fourier Transform)获得的。
- 中心亮点:表示图像的低频成分(整体的平滑变化)。
- 放射状的纹理:表示图像中不同方向的高频细节(例如边缘、锐利的变化)。
- 亮度强弱:频域中每个点的亮度代表该频率分量的强度。
滤波
滤波(Filtering): 去掉特定频率的信息, 某种意义上说,
高通滤波(High-pass filter):保留高频细节,去除低频部分, 得出的是图像的边界信息
低通滤波(Low-pass filter):保留低频整体,去除高频细节, 得出的是模糊的图像
部分频段滤波:保留某个频段的信息, 去除其他频段的信息
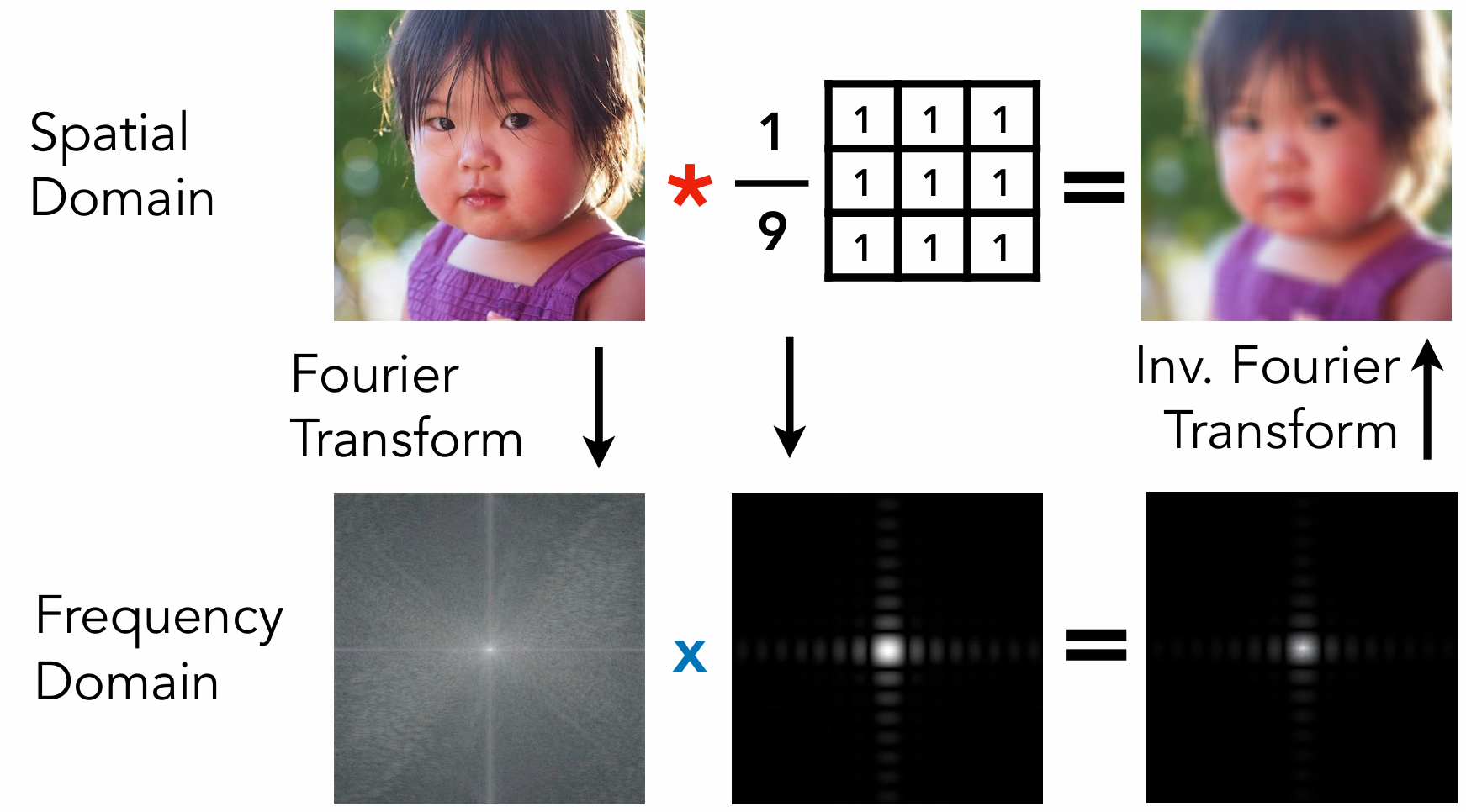
滤波/卷积/平均
时域的卷积等价于频域的乘积
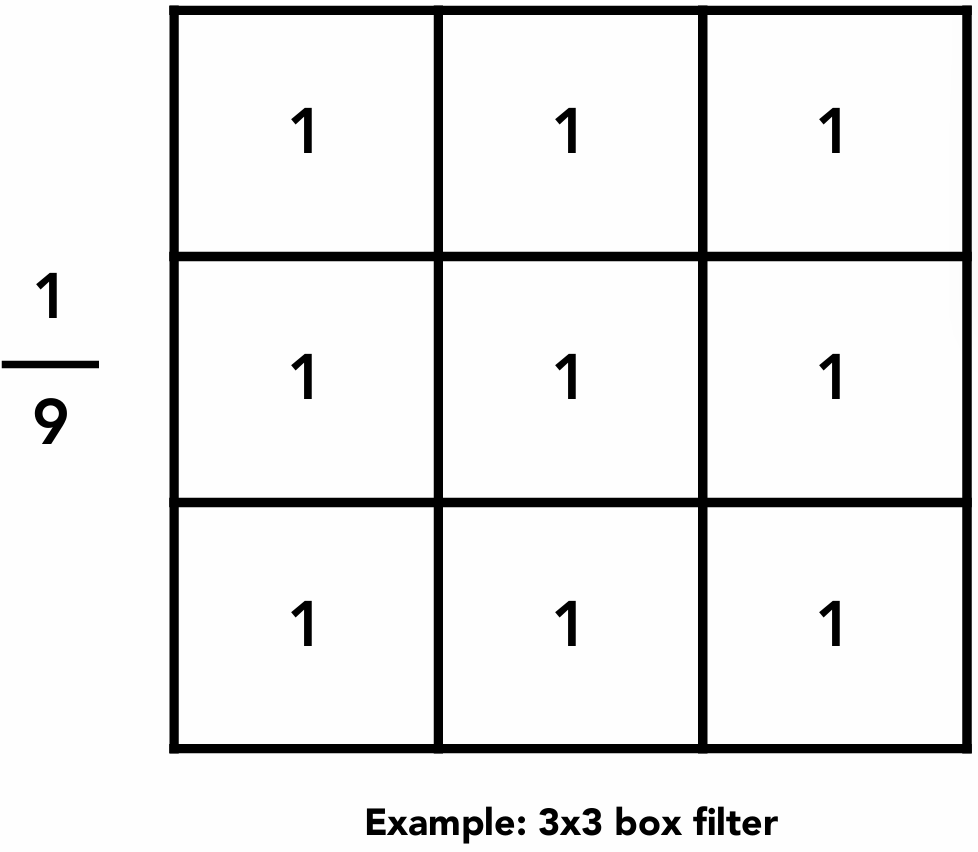
卷积核:
采样与走样的抽象理解
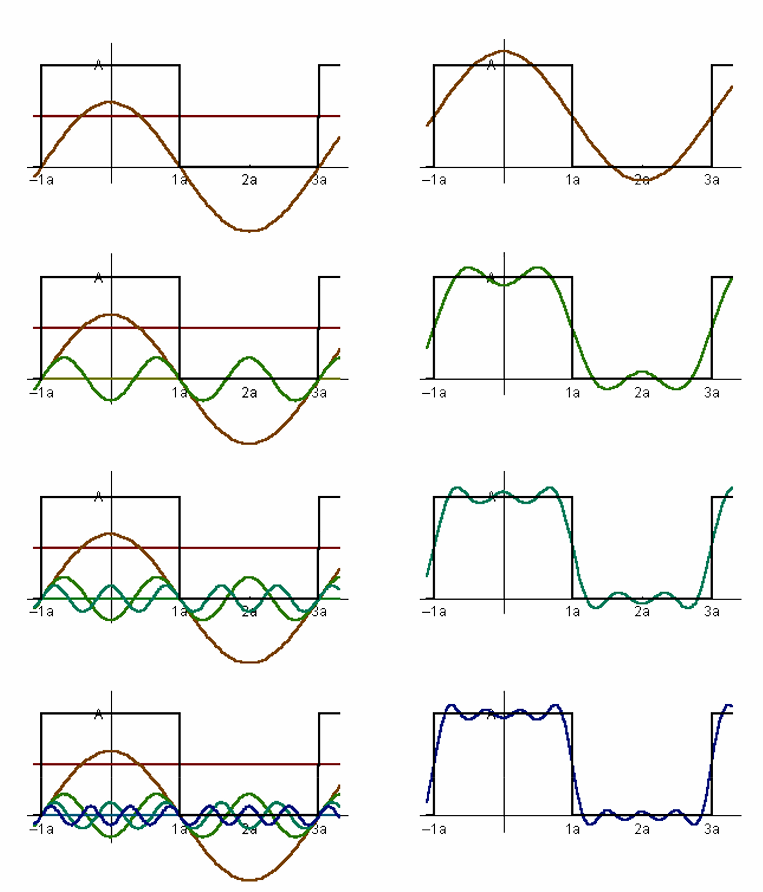
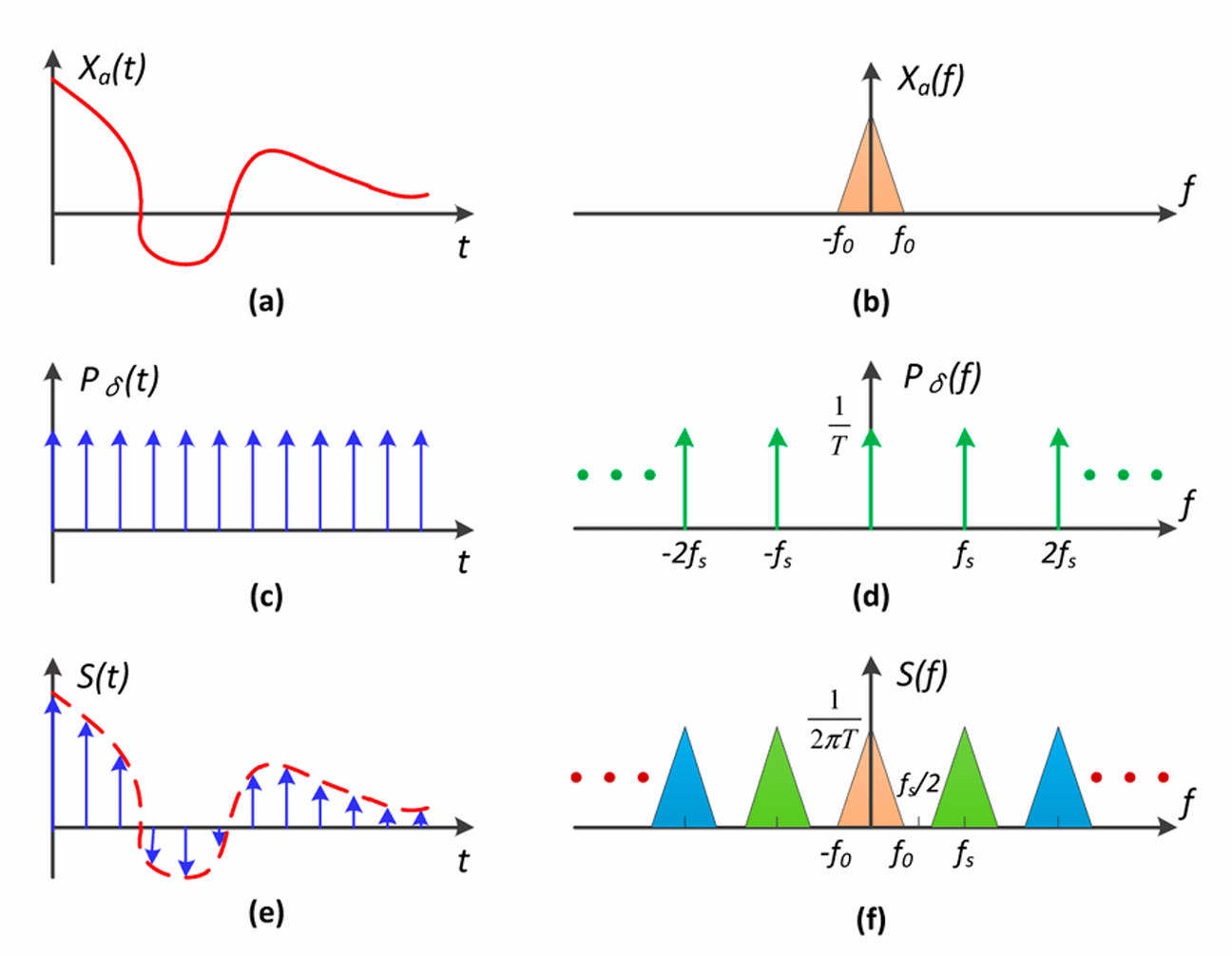
采样是在重复一个原始信号的频谱:
连续的函数在采样后会变成一系列离散的点(a->c->e), 即是在频域上把原始函数的频谱复制粘贴了多次(b->d->f)
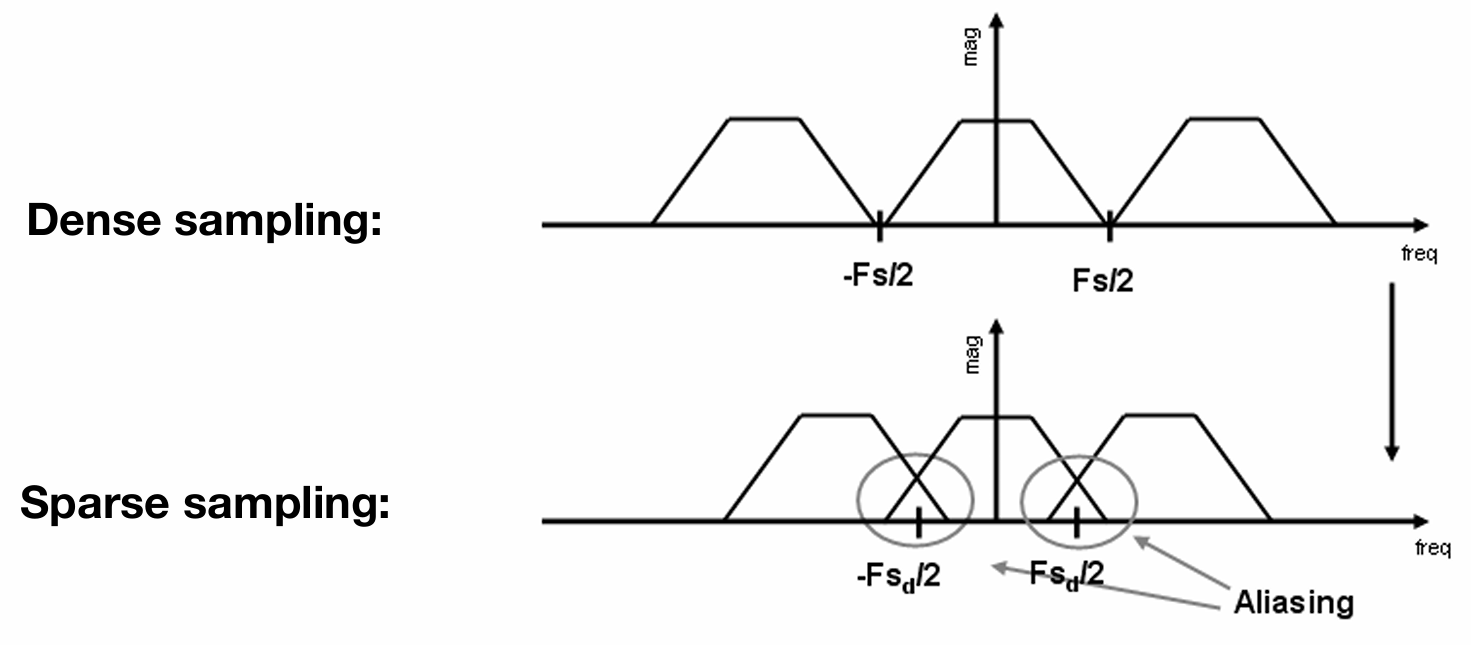
走样: 采样的不同的频率会引起频谱以不同的间隔重复, 如果采样的频率不够高, 频谱的重复的间隔就会较小, 那么就会出现频谱重叠, 从而导致走样
反走样的抽象理解
方法一: 增加采样频率
- 采样频率越高,频谱重复的间隔越大,频谱重叠的可能性越小
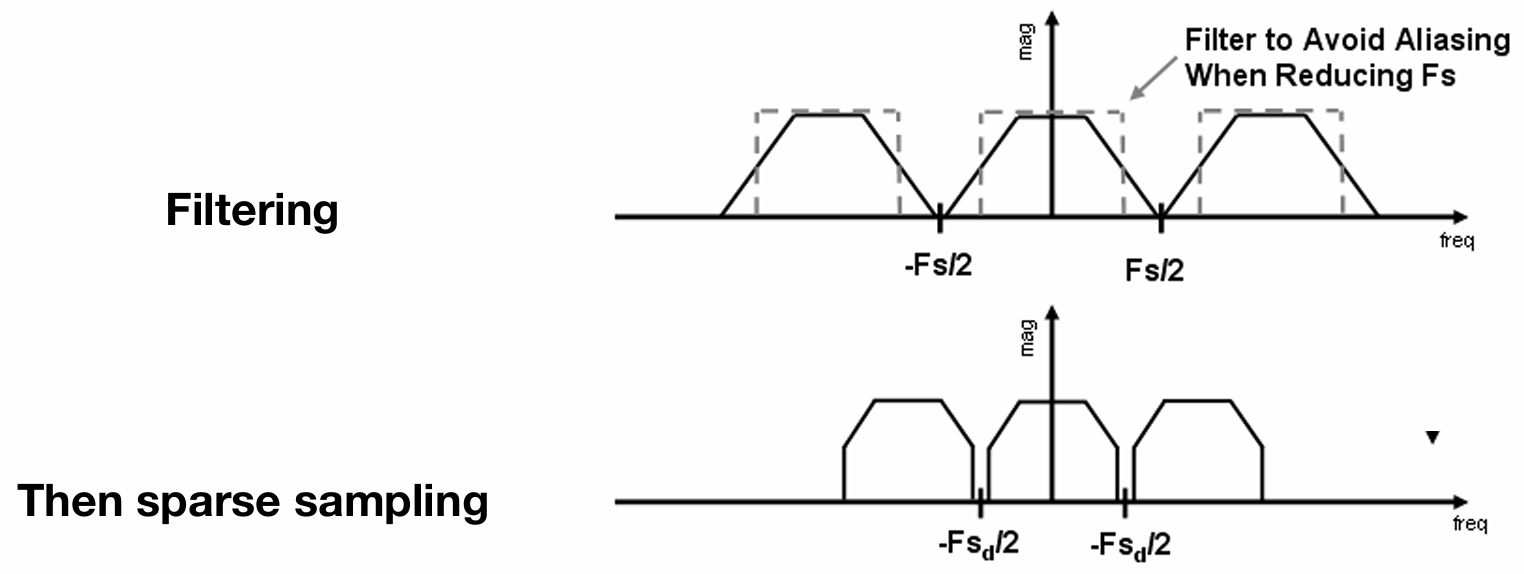
方法二: 先模糊处理, 再采样
- 低通滤波
- 把高频的信息先去掉, 再进行采样, 如下图
抗锯齿的实现
多重采样抗锯齿 MSAA
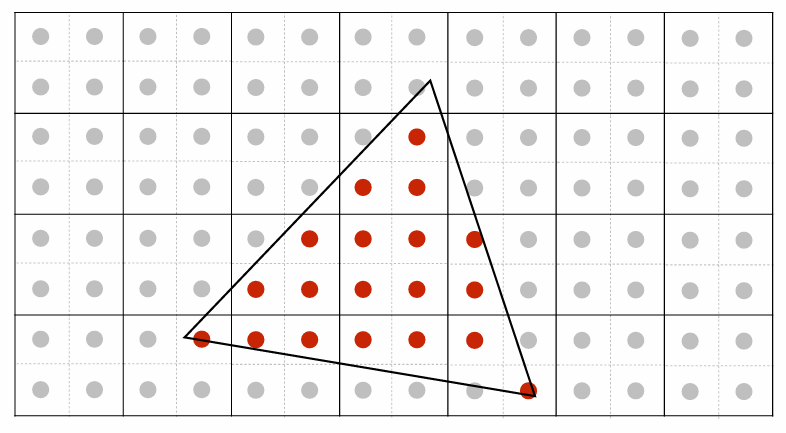
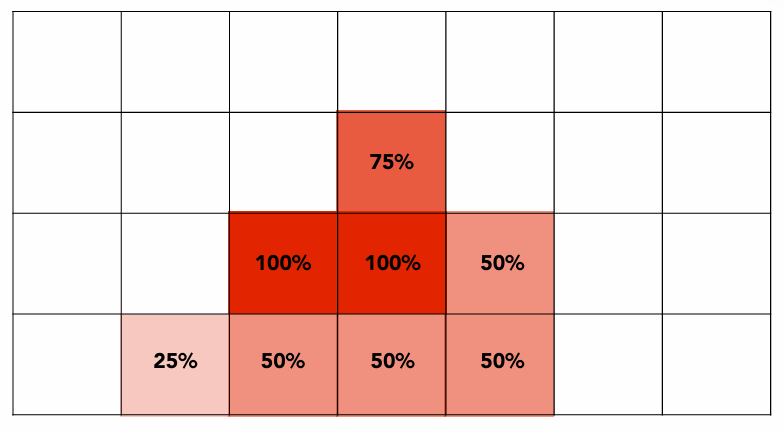
多重采样抗锯齿(Multi-Sample Anti-Aliasing): 将一个像素划分成多个子像素, 对每个子像素进行采样, 从而根据该像素划分的子像素被三角形覆盖的比例来决定该像素的颜色
其他抗锯齿方法
- 快速近似抗锯齿 FXAA (Fast Approximate Anti-Aliasing): 得到有锯齿的图像,然后找到锯齿边界, 对边界进行模糊处理
- 时域抗锯齿 TAA (Temporal Anti-Aliasing): 根据前后帧的信息进行抗锯齿处理
超分辨率
超分辨率(Super-Resolution/Super sampling): 与抗锯齿相反, 但本质相同
- 从低分辨率图像中生成高分辨率图像
- DLSS (Deep Learning Super Sampling): 通过深度学习的方法进行超分辨率处理