GAMES101 第7讲 着色(Blinn-Phong反射模型)
着色的定义
着色(Shading) 在计算机图形学中, 指的是对不同物体应用不同材质的过程.
Blinn-Phong 反射模型
- 高光(Specular Highlights): 比较光滑的物体表面, 会出现类似镜面反射的效果, 反射颜色较亮
- 漫反射(Diffuse Reflection): 光线击中物体表面后, 会均匀地反射到各个方向, 一般是物体表面颜色变换不明显的部分
- 环境光(Ambient Lighting): 在不能被光源直接照射到的区域, 由于光线的多次反射, 会有一些光线被反射到这些区域, 使得这些区域不会完全黑暗
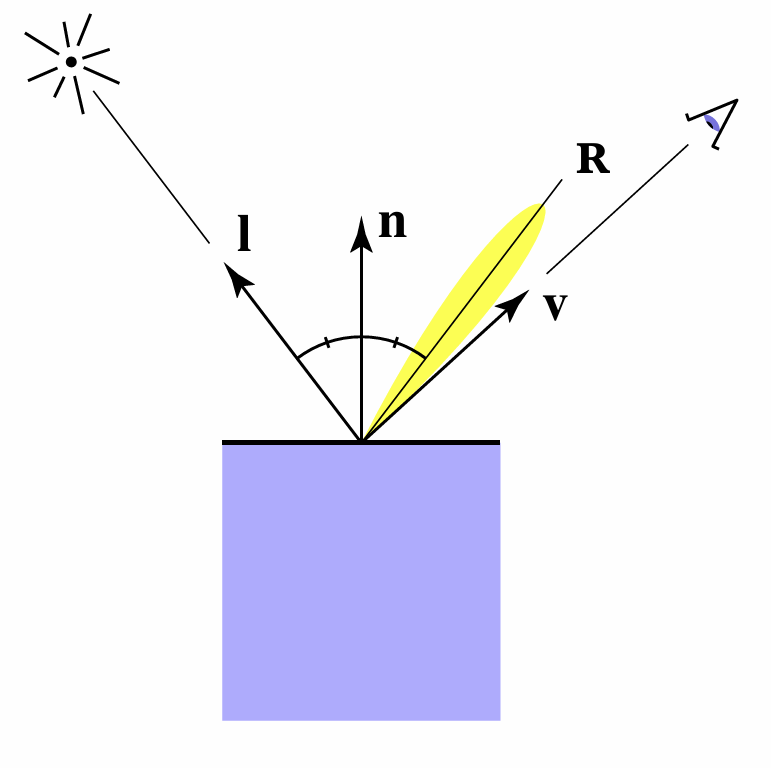
Shading Point 着色点
计算反射到相机的光线颜色时, 是在物体表面上的一个点上进行计算的, 这个点称为着色点(Shading Point).
着色点的参数有:
- 观测点方向(Viewer Direction): 从着色点指向相机的方向, 一般用 $v$ 表示
- 表面法线(Surface Normal): 与表面垂直的方向, 一般用 $n$ 表示
- 光源方向(Light Direction): 从着色点指向光源的方向, 一般用 $l$ 表示, 每个光源都有一个光源方向
- 表面参数(Surface Parameters): 用于计算颜色的参数, 例如颜色, shininess(高光的锐度)等
着色有局部性: 着色(Shading)不等于阴影(Shadow), 不会生成阴影, 只是计算光线反射到相机的颜色
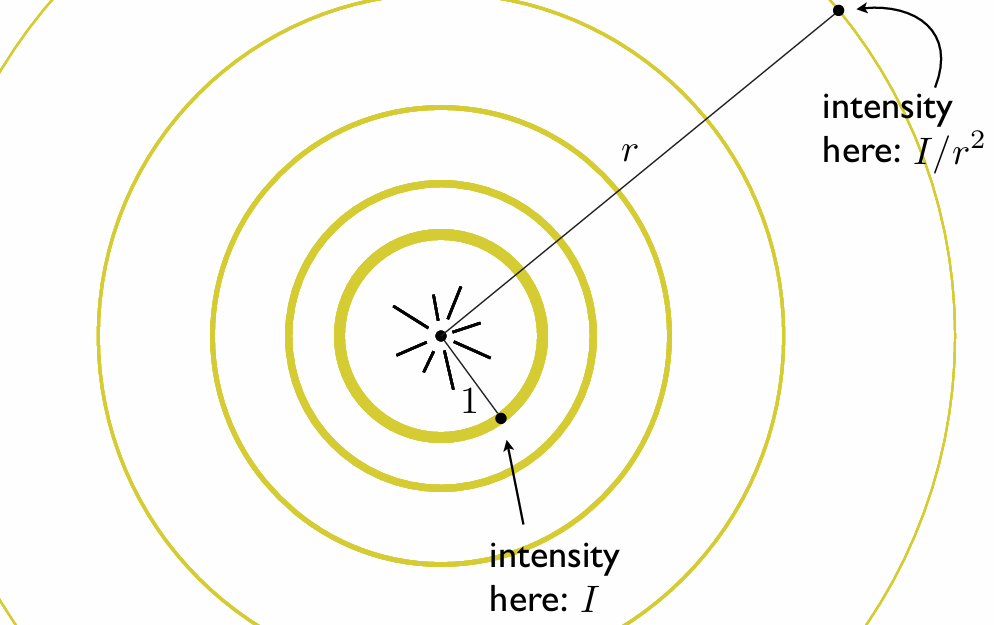
Light Falloff 光线衰减
光线在空间中传播时, 会随着距离的增加而衰减, 这种现象称为光线衰减(Light Falloff).
因为由于能量守恒, 从光源发出的总能量是一定的, 但是距离光源越远, 光照所覆盖的面积就越大, 因此单位面积接收到的光线就会减少:
光线衰减的公式一般为:
\[\text{Intensity} = \frac{Light}{\text{Distance}^2}\]漫反射
漫反射的原理
当一个光线击中物体表面时, 会均匀地反射到各个方向, 这种反射称为漫反射(Diffuse Reflection).
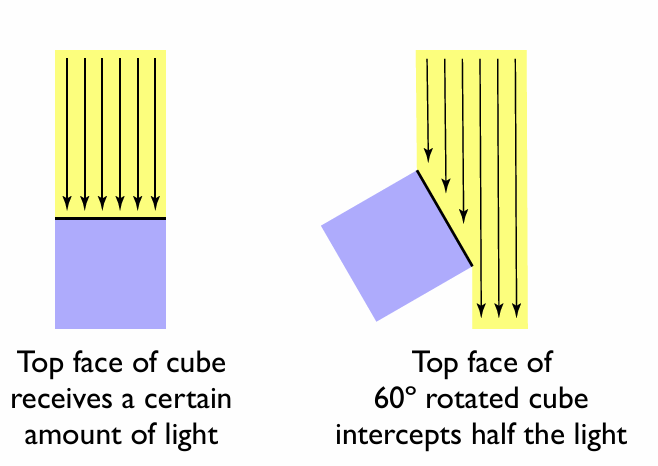
如上图中, 当光线与物体表面成角度时, 不同角度下的光线产生的明暗程度不同, 一般来说, 光线与表面法线的夹角越小, 反射光线越亮.
这是因为, 假设光照可以分解成多个光线, 每根光线都有一定的能量, 当光线垂直于表面时, 物体表面单位面积下会接收到更多的光线, 反射的光线也会更亮; 当物体旋转一定的角度后, 单位面积接受到的光线会减少, 因此反射的光线也会变暗. (如下图)
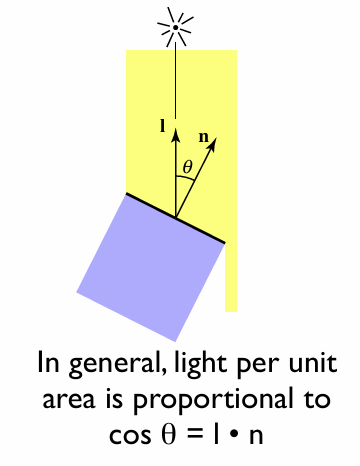
将此过程推广到数学上, 可以得到: 光源方向 $l$ 和表面法线 $n$ 的夹角 $\theta$ 越小, 反射光线的亮度越高.
Lambertian (Diffuse) Shading
Lambertian 漫反射模型是最简单的漫反射模型, 它不依赖于观察方向, 只依赖于光源方向和表面法线:
- $L_d$: 漫反射光线的颜色
- $k_d$: 漫反射系数
- $I$: 光源在单位面积上的光照强度
- $r$: 光源到着色点的距离
- $\mathbf{n}$: 表面法线
- $\mathbf{l}$: 光源方向
漫反射系数 $k_d$: 颜色
$\max(0,\mathbf{n}\cdot\mathbf{l})$: 当两个点乘的结果小于0时, 即光线从表面的下方照射到表面上时, 没有物理意义, 因此取0
高光
平面(物体)比较光滑时, 光线会在表面上沿着镜面反射方向的附近区域反射, 这种现象称为高光(Specular Highlights).
当观察方向与镜面反射方向的夹角越小的时候, 才能看到高光.
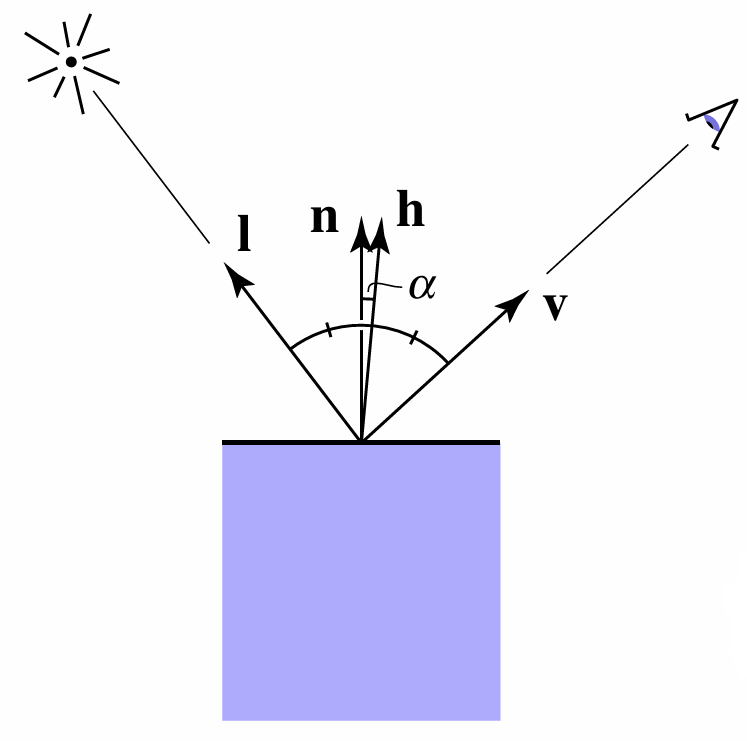
Blinn-Phong 高光模型
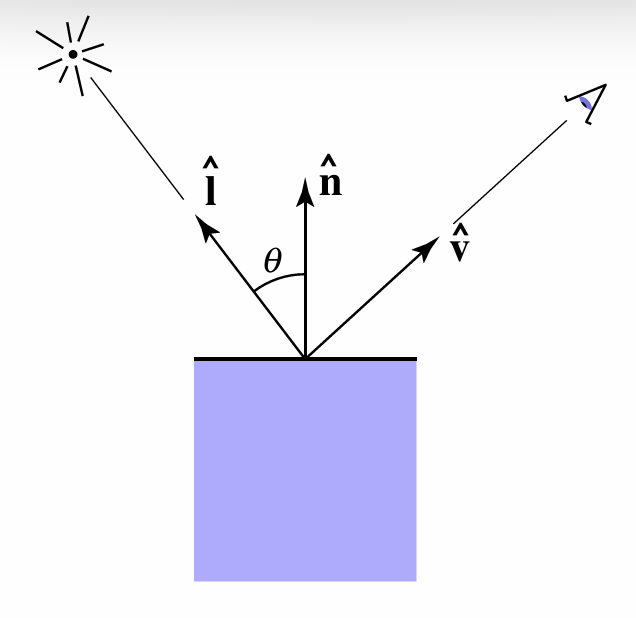
Blinn-Phong 高光模型与上面讲到的高光的原理类似, 但是它引入了一个新的参数, 叫做半程向量(Halfway Vector):
当观察方向和镜面反射方向接近时, 实际上等同于观察方向与光源方向的半程向量 $\mathbf{h}$ 接近于表面法线 $\mathbf{n}$
半程向量是观察方向和光源方向的中间向量, 它通过观察方向和光源方向相加后归一化得到:
\[\mathbf{h}=\frac{\mathbf{v}+\mathbf{l}}{\|\mathbf{v}+\mathbf{l}\|}\]Blinn-Phong 高光模型的公式为:
\[L_s=k_s\left(I/r^2\right)\max(0,\mathbf{n}\cdot\cos\alpha)^{p}\\ L_s=k_s\left(I/r^2\right)\max(0,\mathbf{n}\cdot\mathbf{h})^{\alpha}\]- $L_s$: 高光光线的颜色
- $k_s$: 高光系数:高光的颜色(一般是白色)
- $I$: 光源在单位面积上的光照强度
- $r$: 光源到着色点的距离
- $\mathbf{n}$: 表面法线
- $\mathbf{h}$: 半程向量
- 指数 $p$: 高光的锐度
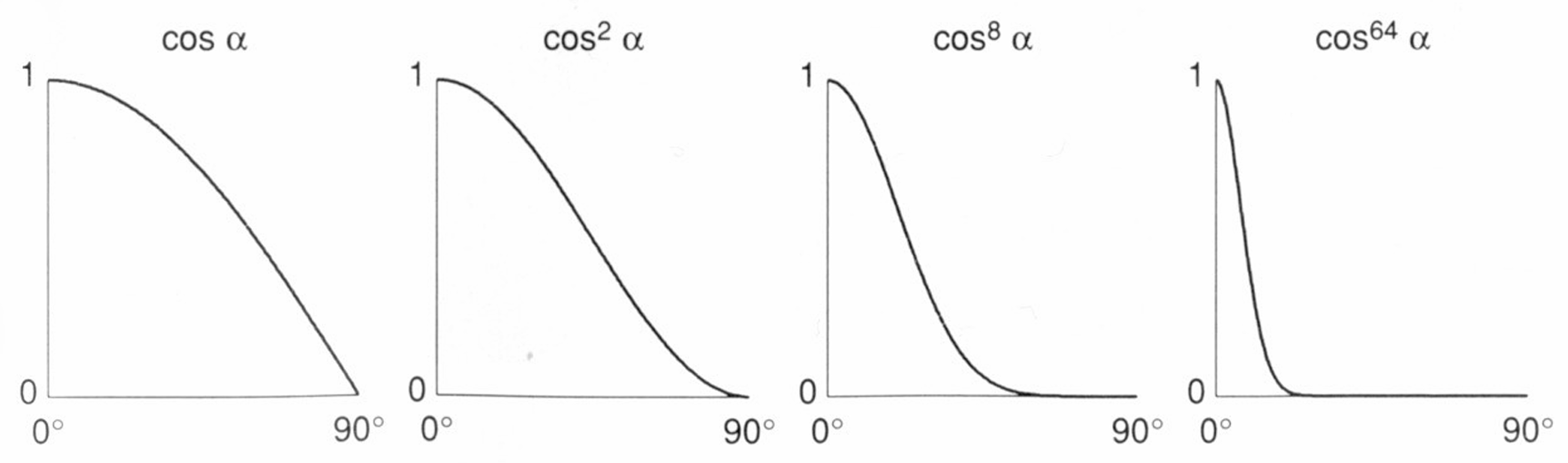
指数p的意义
由于 $\cos\alpha$ 的图象在 $0° ~ 90°$ 之间的变化容忍度太高, 即使角度相差很大, 也会得到较大的值, 而当给 $\cos\alpha$ 取一个较大的指数 $p$ 后, 可以使得高光的锐度更高, 角度相差较大时, 高光的亮度会更低.
Blinn-Phong 高光模型的优点
半程向量与法线的夹角等同于观察方向与光源反射方向的夹角, 但是半程向量的计算更加简单, 且不需要考虑观察方向和光源方向的夹角是否大于90度.
- 半程向量只需要计算两个向量的和, 然后归一化即可
- 光源反射方向的计算需要根据光源方向和表面法线计算
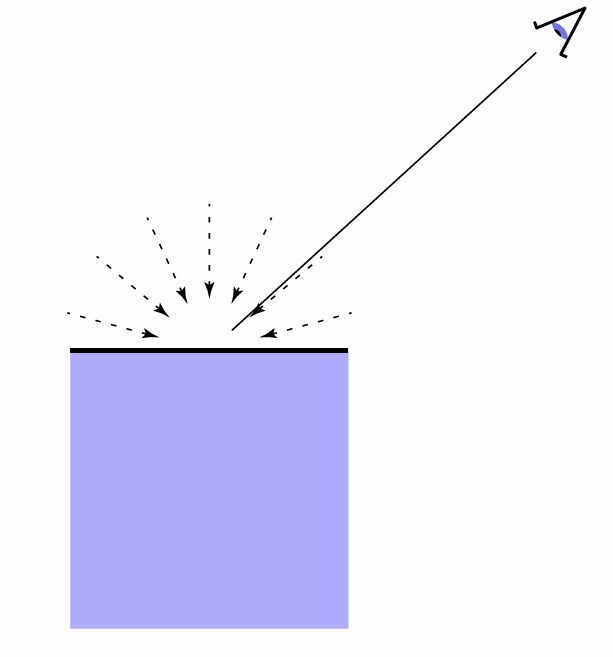
环境光
环境光(Ambient Lighting) 是在不能被光源直接照射到的区域, 由于光线的多次反射, 会有一些光线被反射到这些区域, 使得这些区域不会完全黑暗.
我们假设任何一个点接收到的来自环境的光照的强度永远相同, 则环境光的颜色可以表示为:
\[L_a=k_aI_a\]- $L_a$: 环境光的颜色
- $k_a$: 环境光系数(环境光的颜色)
- $I_a$: 环境光的强度
Blinn-Phong 着色模型的环境光是一个简化的模型, 不能反映真实的环境光, 例如在表面的某个位置出现了凹陷, 凹陷位置的环境光应该比凸起位置的环境光要暗, 但是 Blinn-Phong 着色模型无法反映这种情况, 不过在实际应用中, 由于环境光的影响较小, 因此这种简化的模型也是可以接受的.
Blinn-Phong 着色模型的总合
将漫反射, 高光和环境光的颜色相加, 即可得到 Blinn-Phong 着色模型的颜色:
