GAMES101 第9讲 着色(重心坐标插值, 纹理放大, 纹理缩小)
重心坐标插值
在之前的课程中, 提到了逐顶点着色和逐像素着色, 其中逐顶点着色是在顶点上计算颜色, 然后在三角形内部的像素上对颜色进行插值, 逐像素着色是在每个像素上计算颜色, 但是每个像素的法线也是通过插值得到的.
插值的原因, 内容和方法
重心坐标的计算是为了在三角形内部的像素上进行插值
- 插值的原因: 根据三角形顶点的属性, 可以通过插值得到三角形内部所有点的属性
- 插值的内容: 纹理坐标, 法线, 颜色等
- 插值的方法: 重心坐标插值
重心坐标
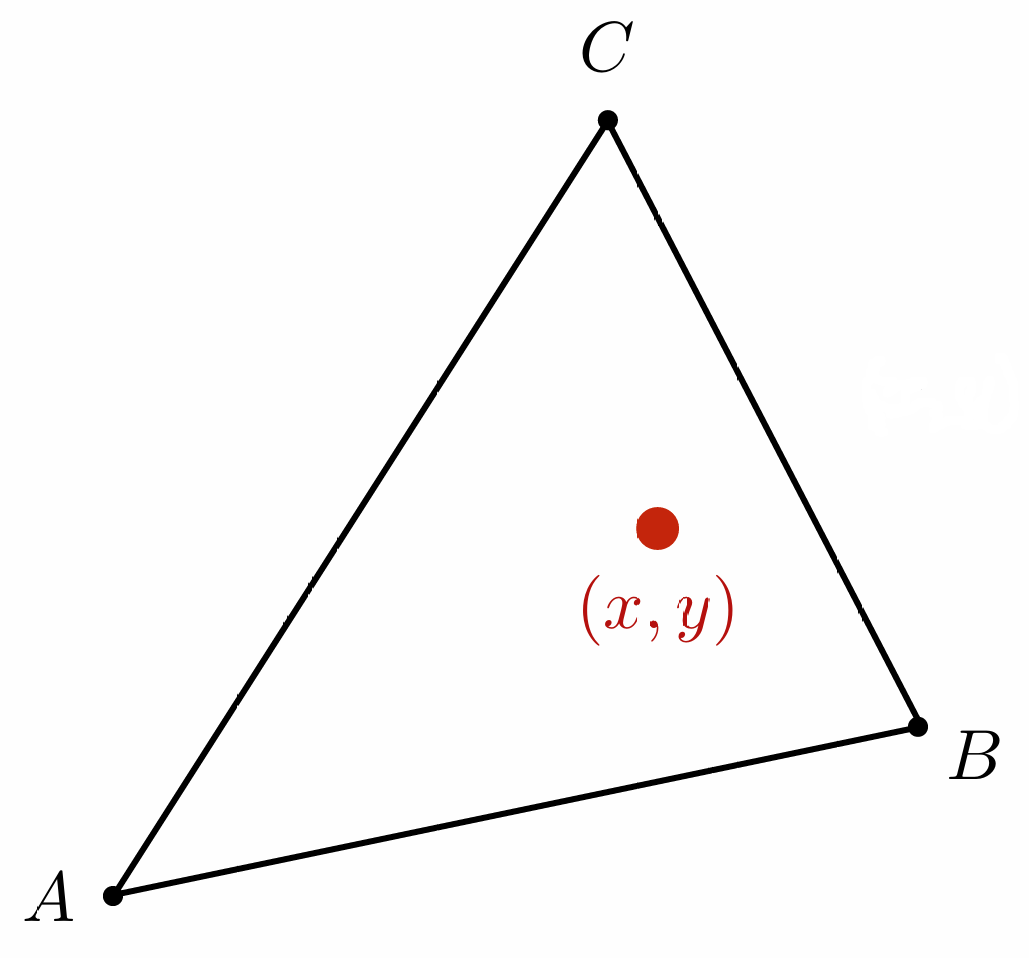
在任意三角形 $ABC$ 中, 内部任意一个点 $(x,y)$ 都可以表示为三个顶点的线性组合:
\[(x,y) = \alpha A + \beta B + \gamma C \quad \text{其中} \quad \alpha + \beta + \gamma = 1\]也就是说, 任意点 $(x,y)$ 在重心坐标系下的坐标为 $(\alpha, \beta, \gamma)$
- 点在三角形平面内: $\alpha, \beta, \gamma = 1$
- 点在三角形边界上: $\alpha, \beta, \gamma = 0$
- 点在三角形内部: $\alpha, \beta, \gamma > 0$
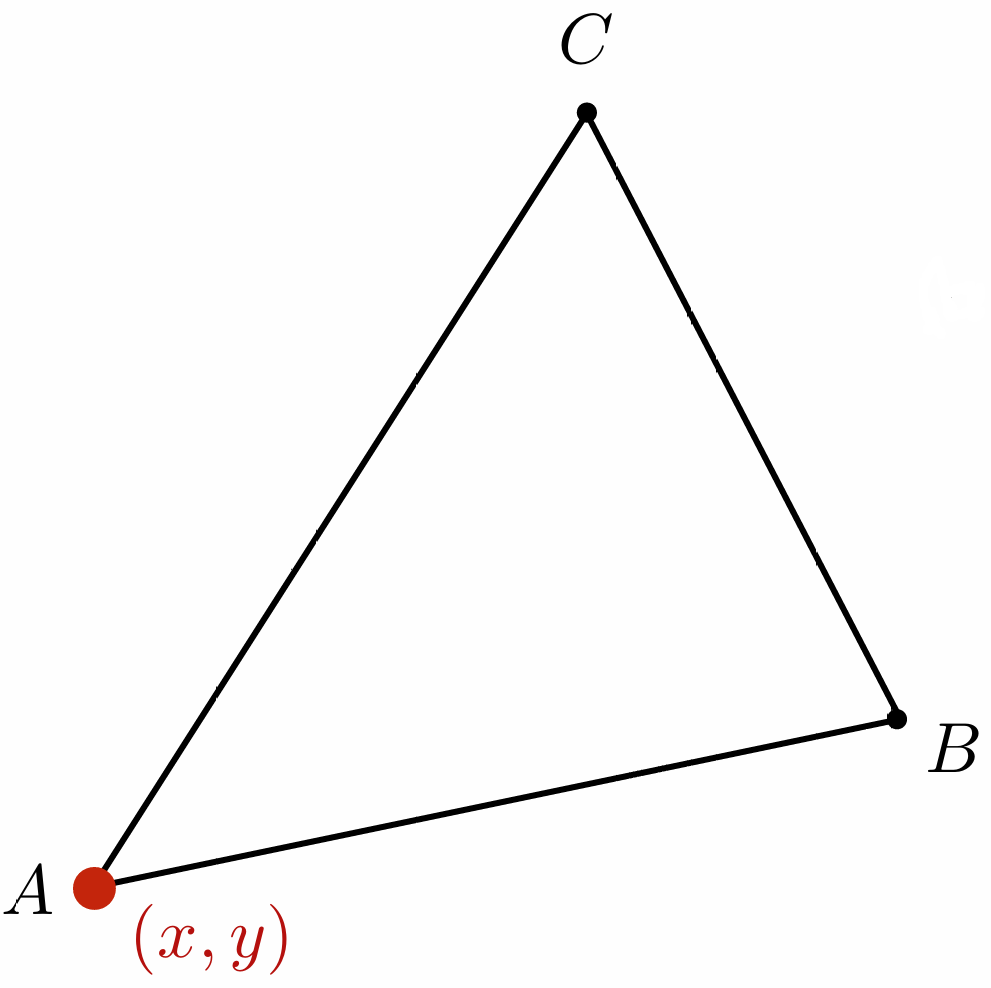
A点自己的重心坐标为 $(1,0,0)$:
- A点的重心坐标为 $(1,0,0)$
- B点的重心坐标为 $(0,1,0)$
- C点的重心坐标为 $(0,0,1)$
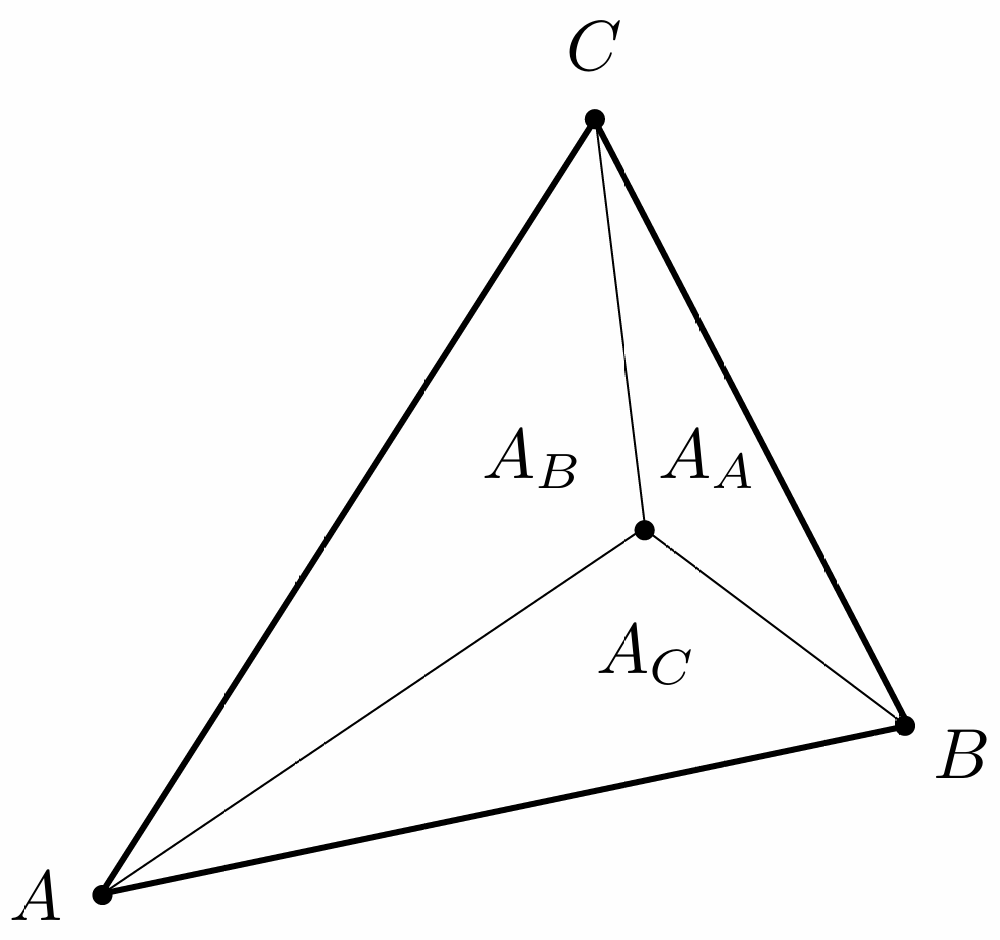
$\alpha, \beta, \gamma$ 的计算
重心
三角形的重心是重心坐标的值为 $(1/3, 1/3, 1/3)$ 的点, 也就是三角形的质心.
\[(\alpha, \beta, \gamma) = (\frac{1}{3}, \frac{1}{3}, \frac{1}{3})\\ (x,y) = \frac{1}{3}A + \frac{1}{3}B + \frac{1}{3}C\]任意点的重心坐标的计算
除了通过面积比例计算重心坐标, 还可以通过以下方法更简化的计算:
对于任意点 $(x,y)$, 给定三角形的三个顶点 $A, B, C$, 坐标分别是 $(x_A, y_A), (x_B, y_B), (x_C, y_C)$, 则:
\[\alpha = \frac {-(x-x_B)(y_C-y_B) + (y-y_B)(x_C-x_B)} {-(x_A-x_B)(y_C-y_B) + (y_A-y_B)(x_C-x_B)}\\ \beta = \frac {-(x-x_C)(y_A-y_C) + (y-y_C)(x_A-x_C)} {-(x_B-x_C)(y_A-y_C) + (y_B-y_C)(x_A-x_C)}\\ \gamma = 1 - \alpha - \beta\]重心坐标插值
假设三角形内部点的属性是 $ V $, 三个顶点的属性分别是 $ V_A, V_B, V_C $, 则三角形内部点的属性 $ V $ 可以通过重心坐标插值得到:
\[V = \alpha V_A + \beta V_B + \gamma V_C\]属性可以是位置,纹理坐标,颜色,法线,深度, 材质等等.
注意: 当某些属性是三维空间的值时, 需要在三维空间中的三角形上进行插值, 而不是在投影后的三角形平面上进行插值.
纹理的应用
屏幕上任意一个采样点(像素中心或MSAA的多个采样点)都有自己的位置 $(x, y)$, 通过这个位置可以计算出纹理坐标$(u, v)$, 然后通过对这个位置上插值出来的 $(u, v)$ 去纹理上查询该点的颜色, 获得颜色后即可对其进行使用(纹理会存储不同的信息, 例如颜色(漫反射系数), 法线等).
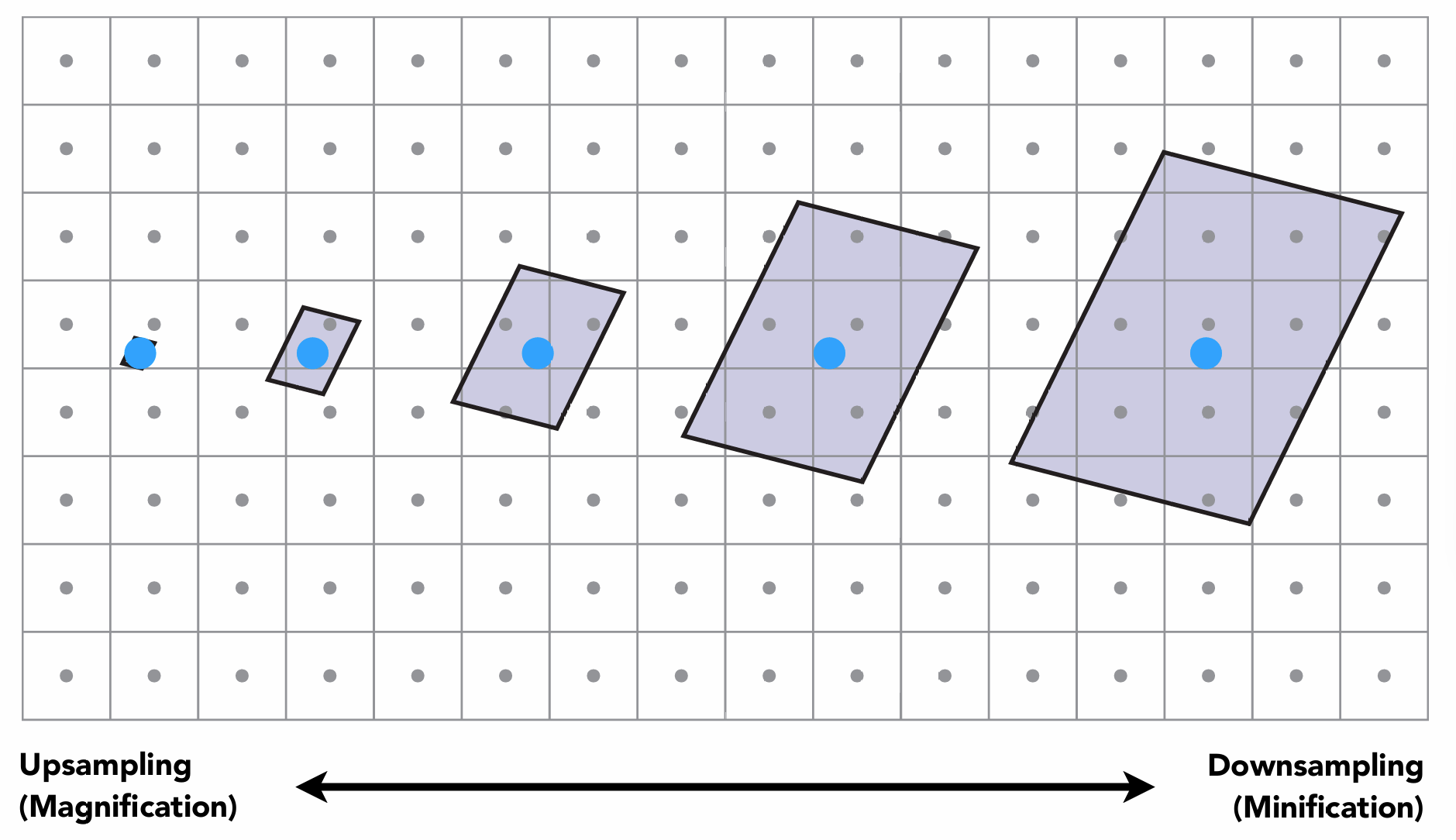
纹理的放大
假如我们准备了一个分辨率较小的纹理, 需要在一个较大的墙面上贴图, 这时就会对纹理进行放大, 得到的效果就是图像会变得模糊或带有锯齿.
- Nearest: 如果任意一个点的纹理坐标不是整数, 则需要将这个点的坐标进行四舍五入, 找到其纹理上的最近的像素点, 然后取这个像素点的颜色作为这个点的颜色.
- Bilinear: 双线性插值, 通过四个最近的像素点的颜色进行插值.
- Bicubic: 利用待采样点周围16个像素点的灰度值进行三次插值计算.
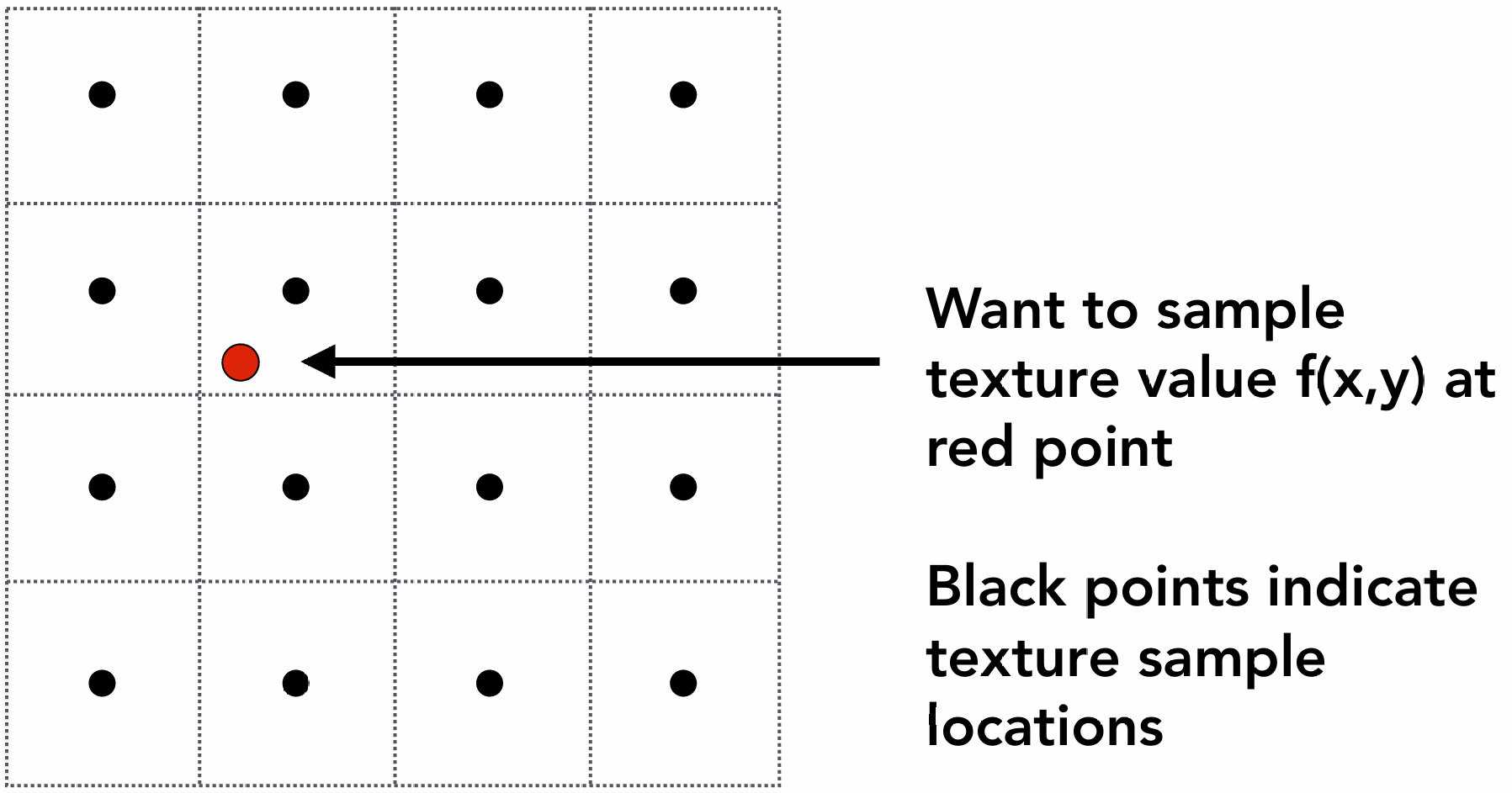
双线性插值 (Bilinear Interpolation)
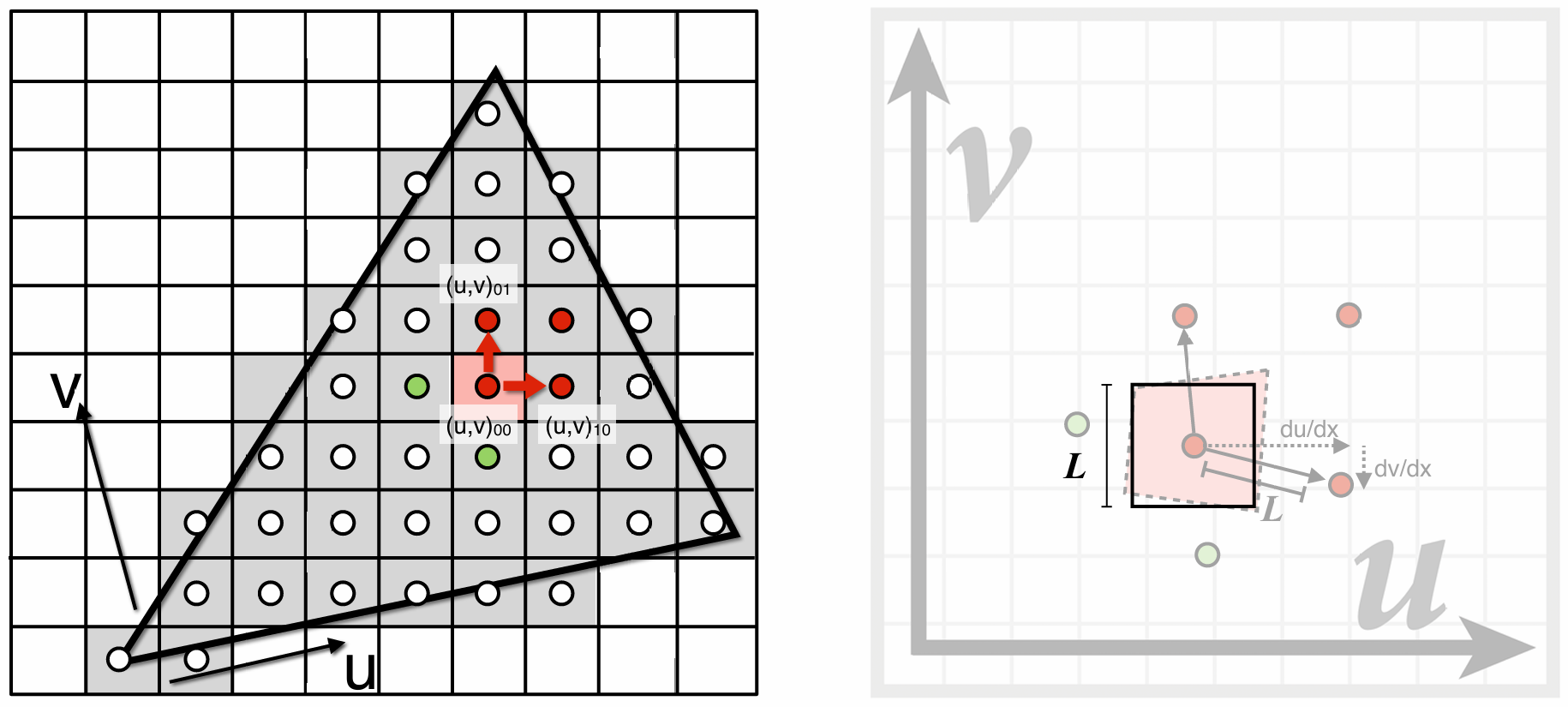
如图, 背景4×4的点是纹理图的像素, 红色的点是采样点, 采样点映射到的纹理坐标不是整数
如果直接选择邻近的像素点的颜色, 则叫做Nearest插值
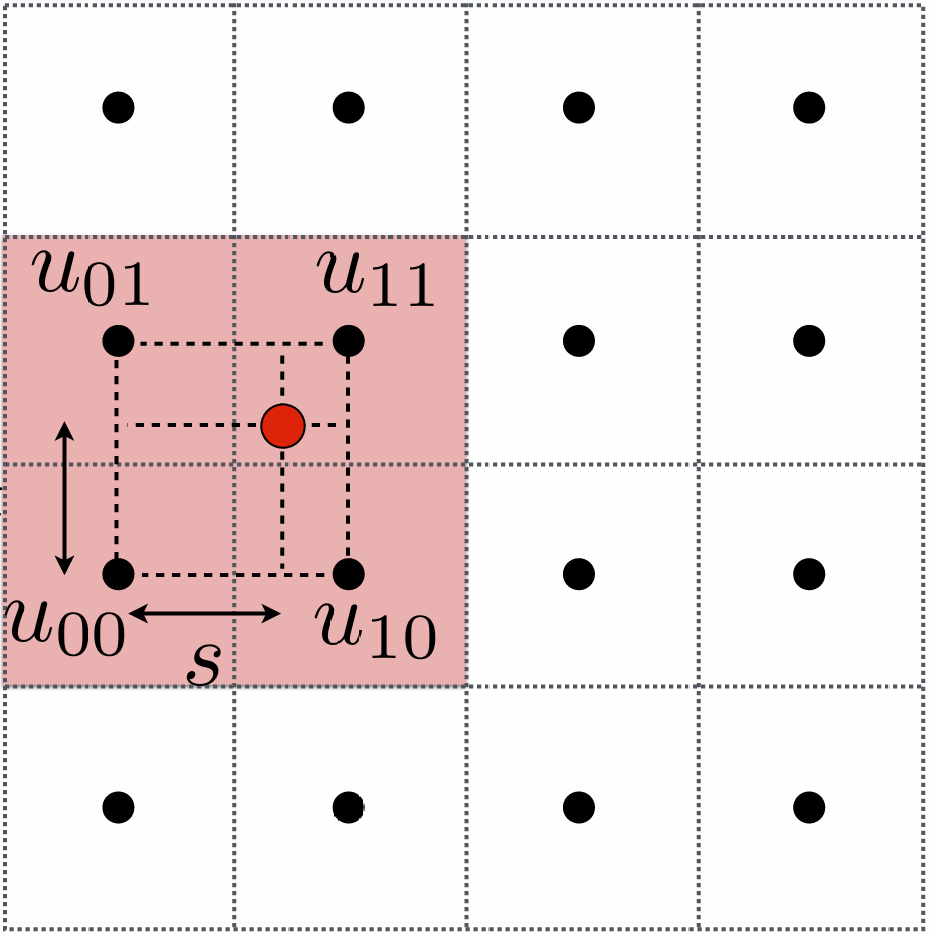
如果选择四个最近的像素点的颜色进行插值, 则叫做Bilinear插值:
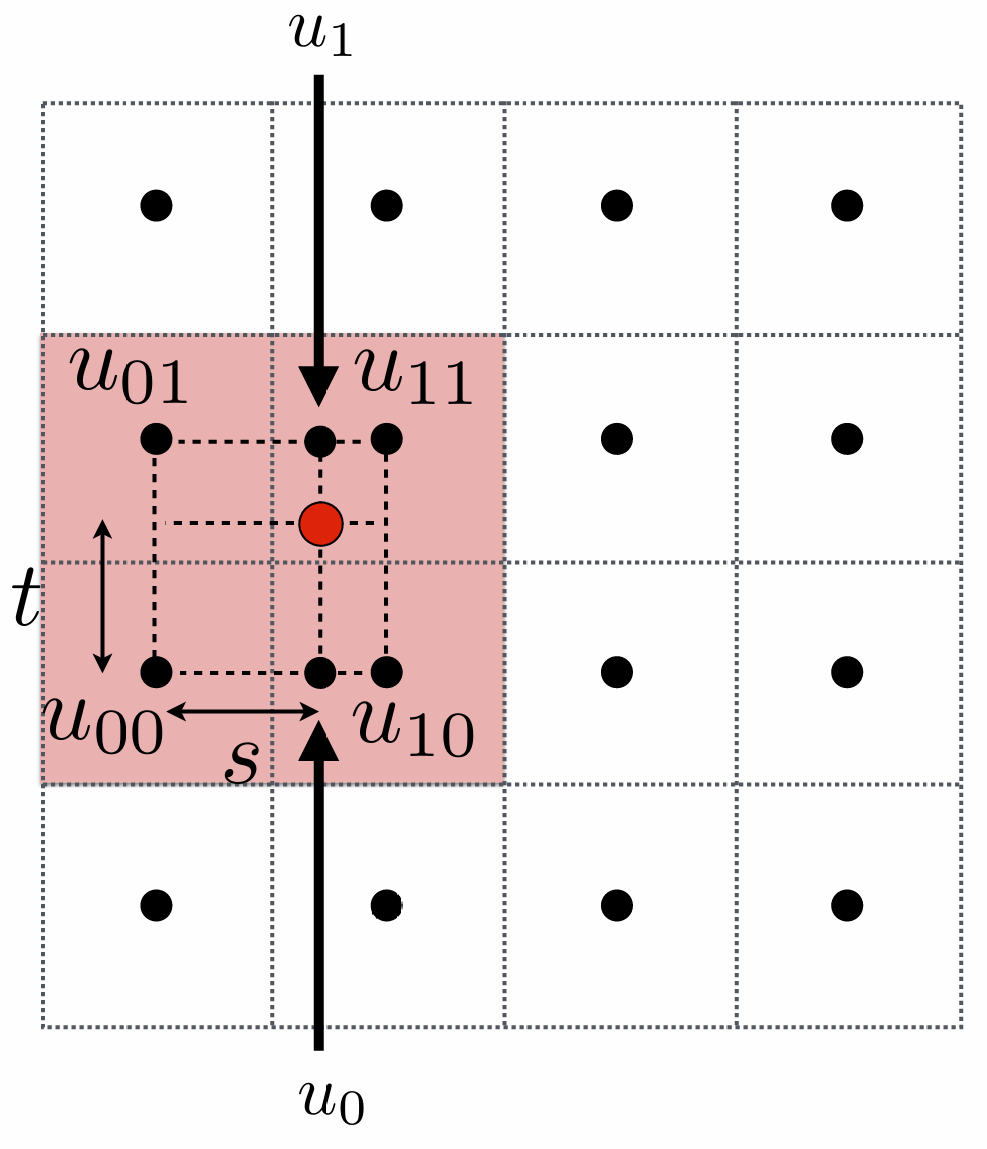
这四个点分别是 $u_00, u_01, u_10, u_11$, 采样点(红点)离左下角的 $u_00$ 的竖直和水平距离分别是 $t$ 和 $s$:
定义一维线性插值操作:
\[lerp(x, v_0, v_1) = v_0 + x(v_1 - v_0)\]
则有
\[u_0 = lerp(s, u_00, u_10)\\ u_1 = lerp(s, u_01, u_11)\]最后, 采样点的纹理颜色为
\[color = lerp(t, u_0, u_1)\]纹理的缩小(纹理太大)
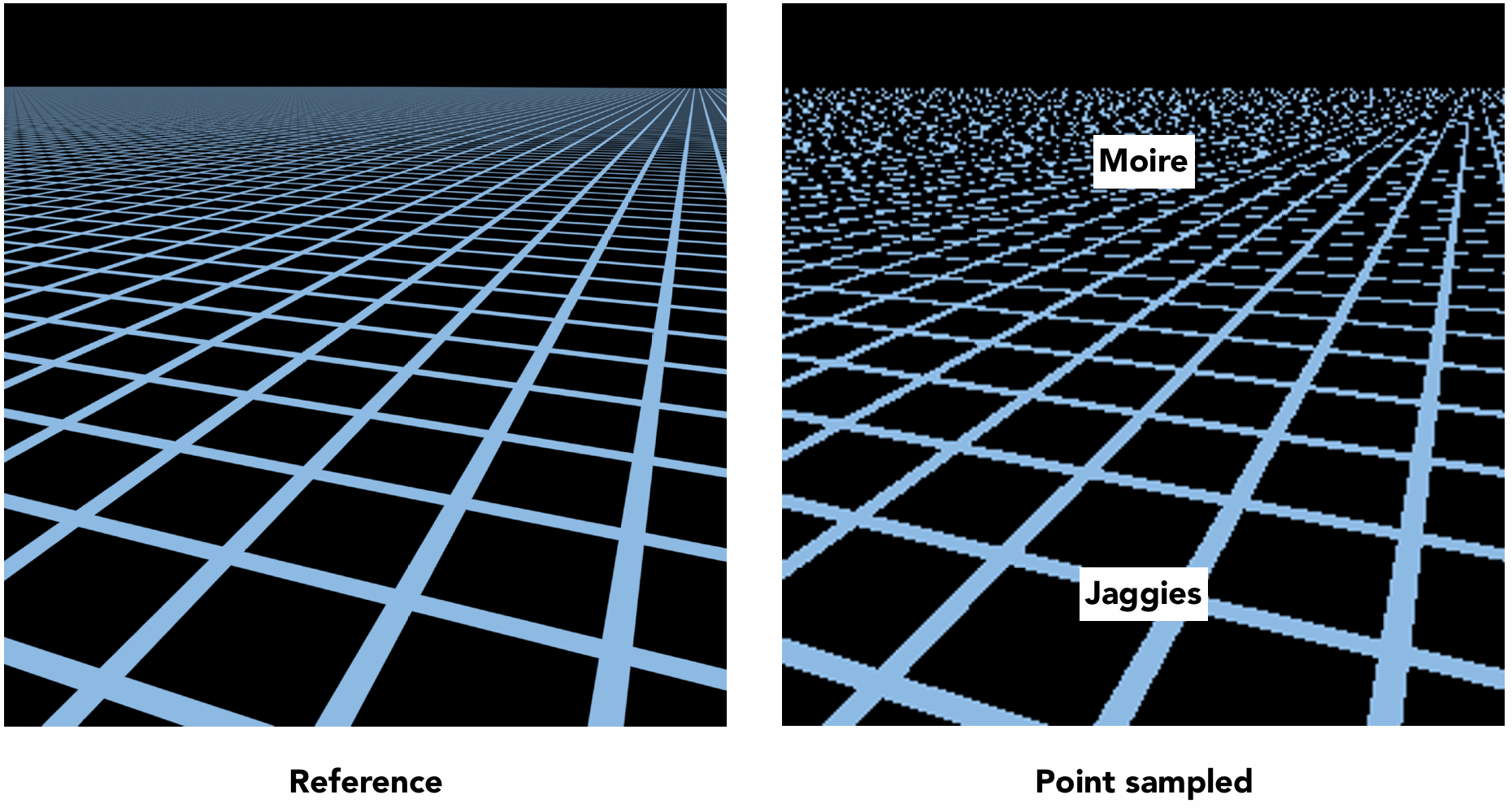
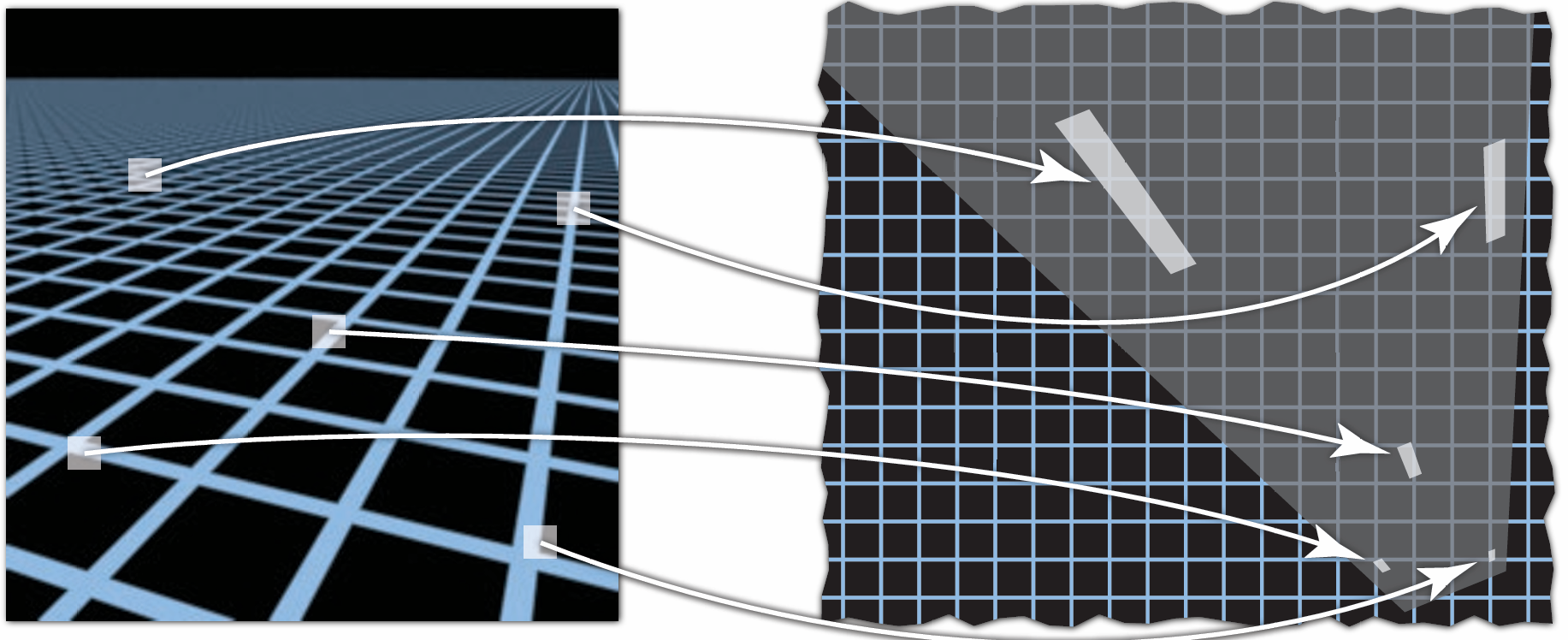
当纹理太大时, 如果不进行处理, 在观察远处的物体时, 会出现纹理失真的情况:
即: 远处出现摩尔纹(Moire Pattern), 近处出现锯齿(Jaggies), 见右图.
这是因为, 在观察近处的物体时, 一个像素覆盖的纹理区域较小, 该像素的采样点在纹理上采样的结果与所该像素覆盖的纹理区域所含像素一样(或接近), 得到的效果和预期值相比较为准确
但是, 在观察远处物体时, 一个像素覆盖率一片纹理, 采样点却仍然只采样附近的纹理像素的颜色, 与真实情况所期望的(所覆盖的一片纹理的颜色平均值)有较大差别, 所以得到的效果较差
Mipmap
如果可以不进行采样, 即直接知道像素所覆盖的纹理区域的平均颜色, 而不用根据采样点及其附近的纹理像素的颜色来计算, 则可能可以得到更好的效果.
为了解决纹理缩小的问题, 可以使用Mipmap技术, 即为纹理生成一系列不同分辨率的纹理, 从而在不同距离的物体上使用不同分辨率的纹理, 从而得到更好的效果.
Mipmap的特性:
- 快
- 不准确
- 方形范围
每张大一层级的Mipmap纹理是由上一层级的纹理缩小得到的, 边长的像素量减少为原来的一半, 总像素量减少为原来的四分之一, 每一层级以此类推, 直到最小的一张纹理为1×1的像素.
Mipmap的占用空间为:
\[\text{Mipmap总占用空间} = \text{原始纹理占用空间} \times \frac{4}{3}\]计算Mipmap的Level $D$
根据采样点相邻的纹理像素的距离, 可以计算出在纹理坐标系下的两个采样点的距离:
\[L = max(\sqrt{(\frac{du}{dx})^2 + (\frac{dv}{dx})^2},\sqrt{(\frac{du}{dy})^2 + (\frac{dv}{dy})^2})\]这里计算的 $L$ 将会作为一个正方形的边长, 用来计算Mipmap的Level $D$, 这个正方形将会是这一层的Mipmap纹理的像素:
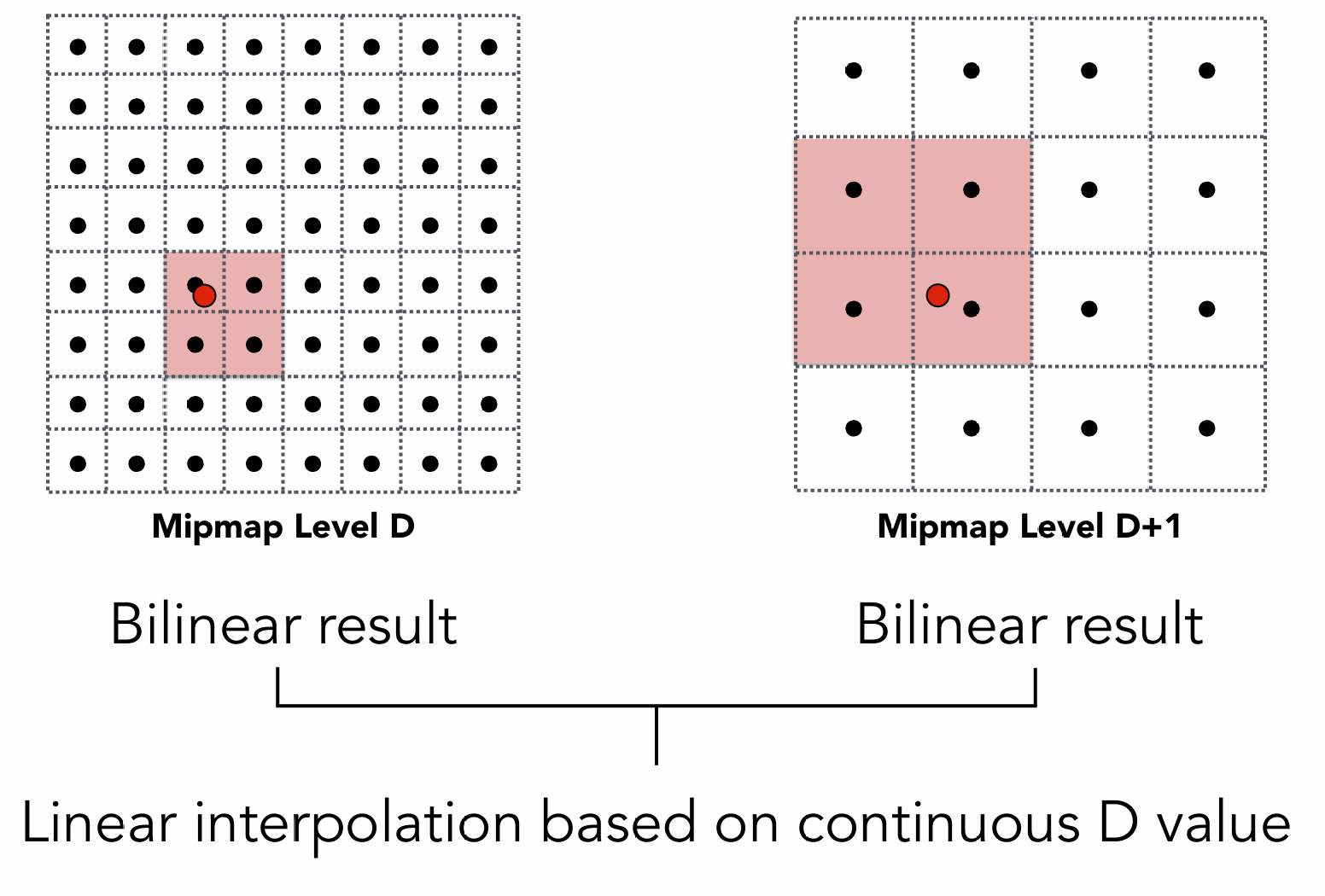
\[D = log_2(L)\]但是, 这样的结果不连续:
如果我们想要得到连续的结果, 可以使用两个Mipmap Level 之间的结果进行插值:
根据两次线性插值的结果, 然后再进行一次线性插值, 就可以得到连续的结果, 被称为三线性插值 Trilinear Interpolation.
各向异性过滤(Anisotropic Filtering)
如果直接按照前文所说的方法进行Mipmap的计算, 很容易出现Over blur的情况, 即纹理的细节丢失过多, 从而导致纹理失真: 远处的纹理糊成一片
为了解决这个问题, 可以使用各向异性过滤(Anisotropic Filtering), 通过对纹理的各个方向进行不同程度的缩小, 从而得到更好的效果.
比起Mipmap, 各向异性过滤多了水平和垂直方向的单独的缩小比例, 从而得到更好的效果.
