GAMES101 第9讲 着色(环境光照, 法线贴图)
纹理不但可以用来表示物体的颜色, 还可以用来记录很多信息.
环境光照
将任何一个方向来源的光照都记录下来, 保存在一个贴图中, 这个贴图就是环境光照贴图.
环境光也可以记录在一个球面上, 这个球面就是环境光照球(Spherical Environment Map)
环境光球展开后可以得到如下的图象:
展开后, 我们可以看到, 在上下边缘部分, 会有较大的扭曲, 为了解决这个问题, 我们可以使用立方体贴图 Cube Map.
立方体贴图是一个立方体, 展开后可以得到如下的图象:
好处是, 立方体贴图的展开后, 没有扭曲, 但是坏处是计算光照的时候, 不能像球面那样直接计算, 需要进行一些额外的计算.
法线贴图/凹凸贴图
纹理可以记录物体表面为基准时, 向上或向下的偏移量, 也就是相对的高度的信息, 这种纹理叫做凹凸贴图 Bump Map, 也可以记录物体表面的法线信息, 这种纹理叫做法线贴图 Normal Map.
也就是说, 我们不需要把几何模型制作的很复杂, 只需要在纹理上记录高度信息(或法线信息), 就可以让物体看起来很复杂.
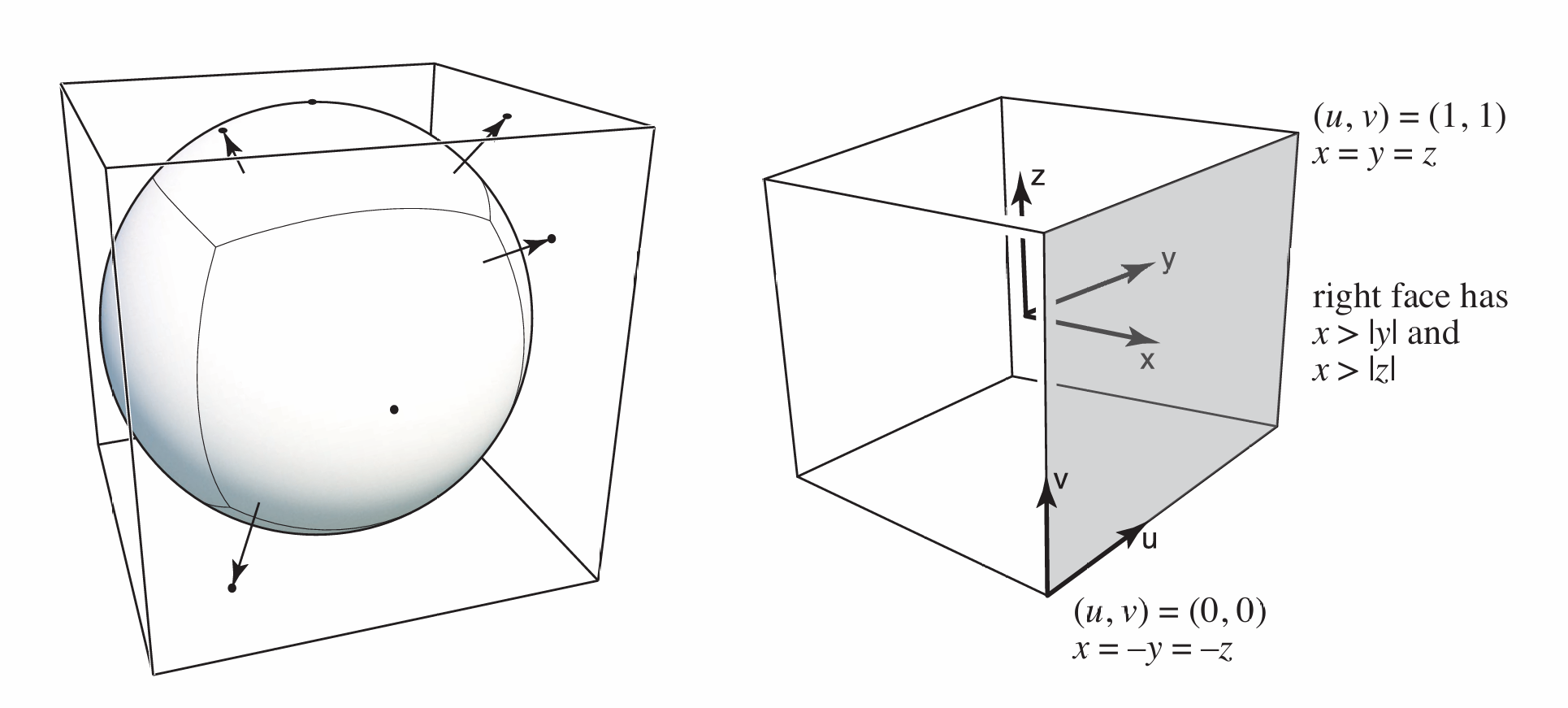
法线贴图的原理
在表面上任意一个点的法线(不是法线贴图的法线值), 我们假设是 $n(p) = (0, 0, 1)$, (这是假设在局部坐标系里的法线)
\[\frac{dp}{du} = c1 * [h(\mathbf{u}+1) - h(\mathbf{u})] \\ \frac{dp}{dv} = c2 * [h(\mathbf{v}+1) - h(\mathbf{v})]\]其中
- $p$ 是表面上的一个点
- $c1, c2$ 是常数, 控制在 $u, v$ 方向上的偏导数的缩放比例
- $h(u)$ 是高度函数
- $\frac{dp}{du}$ 是 $p$ 在 $u$ 方向上的变化率
- $\frac{dp}{dv}$ 是 $p$ 在 $v$ 方向上的变化率
以此可以计算出 $p$ 点的法线 $n$:
\[n = (-\frac{dp}{du}, -\frac{dp}{dv}, 1).normalized()\]位移贴图
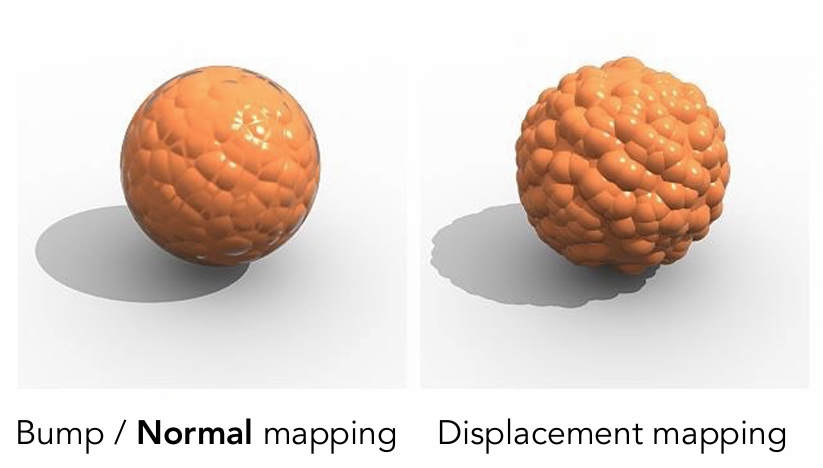
位移贴图 Displacement Map 是一种特殊的凹凸贴图, 它不仅可以改变表面的法线, 还可以改变表面的位置: 位移贴图会真正的移动表面顶点的位置.
代价: 要求模型本身的三角面片要足够密集
纹理的其他应用
预计算着色
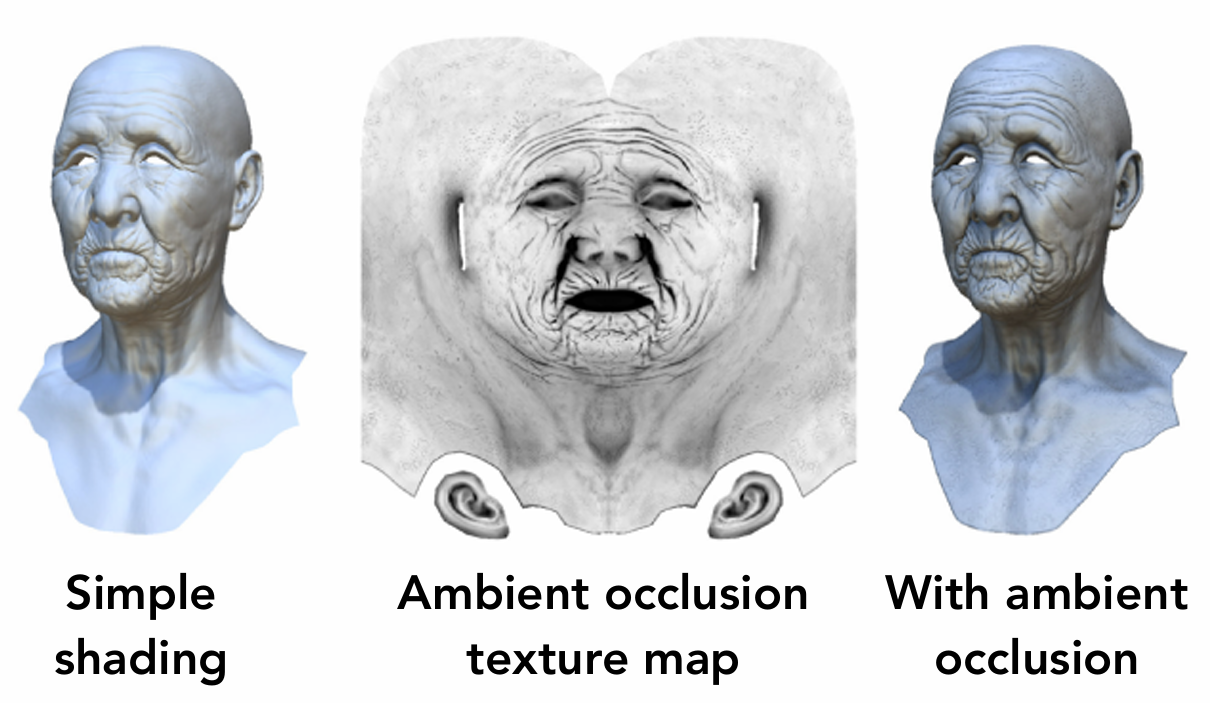
预计算着色 Precomputed Shading 是一种在离线渲染时, 预先计算好光照信息, 保存在纹理中, 在实时渲染时, 直接使用这些纹理.
例如: 环境光遮蔽(Ambient occlusion)贴图:
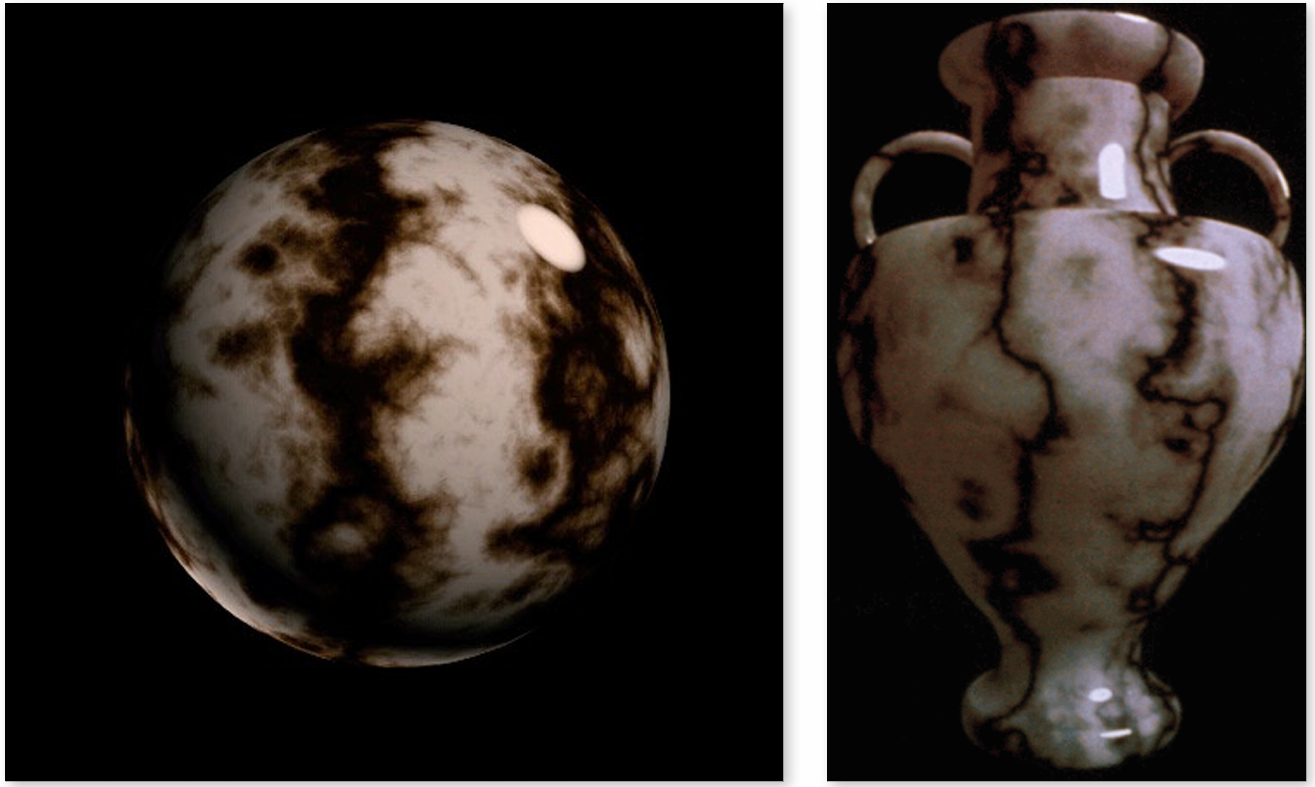
三维纹理
三维纹理 3D Texture 定义了空间中任意一点的值, 通常用来表示体积数据.
